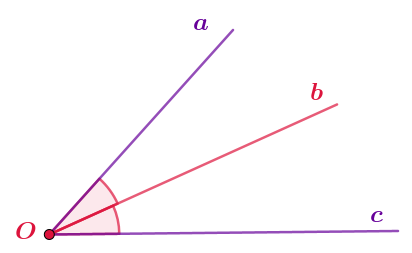
На рисунке несколько лучей с общим началом. Отмечены равные углы.
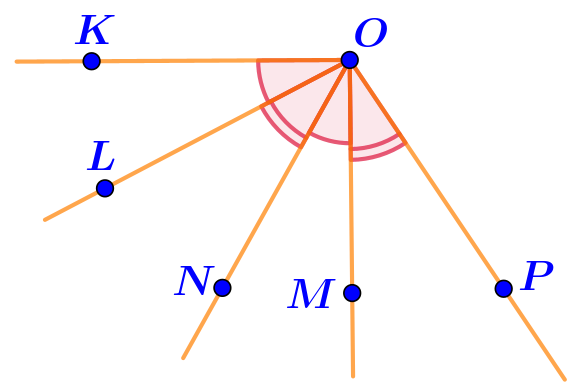
Какой луч является биссектрисой угла \(\displaystyle KOP{\normalsize ?}\)
По рисунку наиболее подходящим кажется луч \(\displaystyle ON{\small .}\)
По разные стороны его продолжения изображены и обозначены равные углы.
Если две части, из которых составлен угол, соответственно равны двум частям, из которых составлен другой угол, то углы равны.
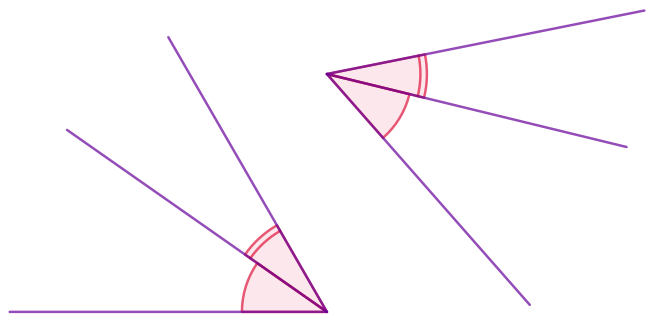
На рисунке два угла. Две части одного из них соответственно равны двум частям второго.
Из этого следует, что и сами углы равны.
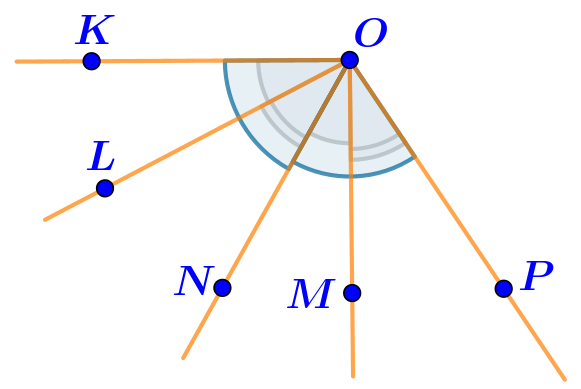
В нашем случае углы \(\displaystyle KON\) и \(\displaystyle NOP\) составлены из двух пар равных углов:
| УГОЛ | \(\displaystyle \angle KON\) | \(\displaystyle \angle NOP\) | |
| Первая часть угла | \(\displaystyle \angle KOL\) | \(\displaystyle =\) | \(\displaystyle \angle NOM\) |
| Вторая часть угла | \(\displaystyle \angle LON\) | \(\displaystyle =\) | \(\displaystyle \angle MOP\) |
Значит и сами углы равны:
\(\displaystyle \angle KON=\angle NOP{\small .}\)
То есть луч \(\displaystyle ON\) действительно является биссектрисой угла \(\displaystyle KOP{\small .}\)
Ответ: \(\displaystyle ON{\small .}\)