Задание
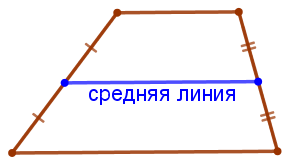
На клетчатой бумаге с размером клетки \(\displaystyle 1×1\) изображена трапеция. Найдите длину средней линии этой трапеции.
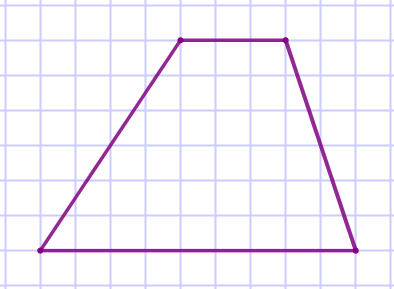
Решение
СПОСОБ \(\displaystyle 1{\small.}\) По определению.
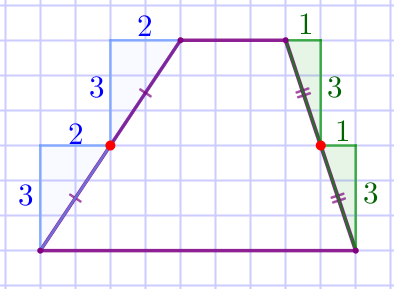
Отметим на рисунке середины сторон трапеции.
Соединим середины боковых сторон трапеции отрезком. По рисунку видим, что длина средней линии равна \(\displaystyle 6{\small.}\) | 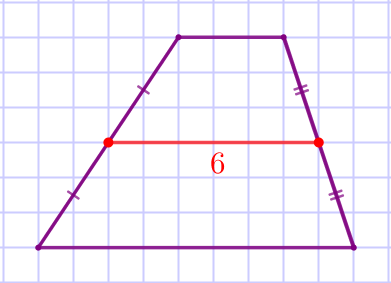 |
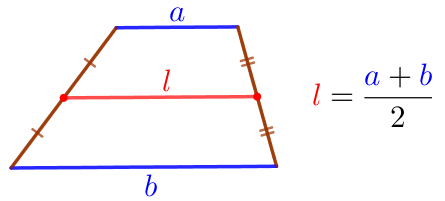
СПОСОБ \(\displaystyle 2{\small.}\) По теореме о средней линии трапеции.
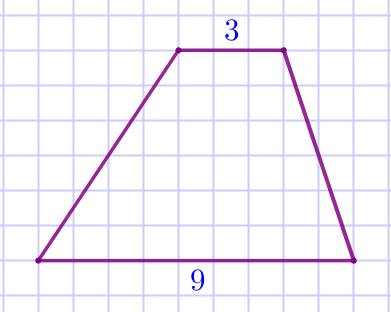 | По рисунку определим длины оснований трапеции:
Значит, длина средней линии трапеции равна \(\displaystyle \frac{3+9}{2}=\frac{12}{2}=6{\small.}\) |
Ответ: \(\displaystyle 6{\small.}\)