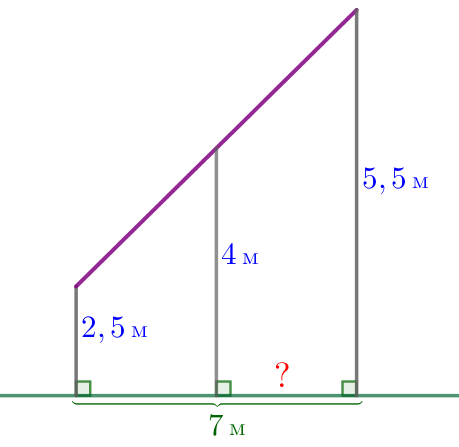
Наклонная крыша установлена на трёх вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит между малой и большой опорами. Высота малой опоры – \(\displaystyle 2{,}5\, \footnotesize м{\small,}\) высота средней опоры – \(\displaystyle 4\, \footnotesize м{\small,}\) высота большой опоры – \(\displaystyle 5{,}5\, \footnotesize м{\small.}\) Найдите расстояние между средней и большой опорами, если расстояние между малой и большой опорами равно \(\displaystyle 7\, \footnotesize м{\small.}\)
\(\displaystyle \footnotesize м{\small.}\)
Изобразим предложенную в задаче конструкцию в виде прямоугольной трапеции \(\displaystyle ABCD{\small:}\)
Требуется найти \(\displaystyle ND{\small.}\) | 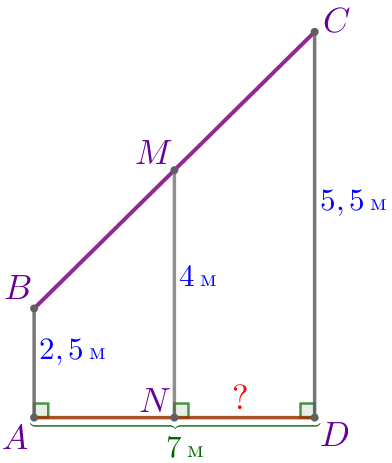 |
\(\displaystyle MN\) – средняя линия трапеции \(\displaystyle ABCD{\small.}\)
Если в трапеции отрезок, соединяющий боковые стороны, параллелен основаниям и его длина равна полусумме оснований, то этот отрезок является средней линией данной трапеции. | 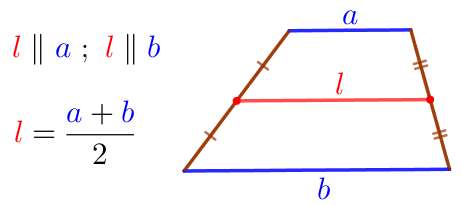 |
Заметим, что:
\(\displaystyle \color{red}{1)}\) \(\displaystyle AB \perp AD{\small,}\) \(\displaystyle CD \perp AD\) и \(\displaystyle MN \perp AD{\small,}\) следовательно,
\(\displaystyle MN \parallel AB\) и \(\displaystyle MN \parallel CD{\small.}\)
\(\displaystyle \color{red}{2)}\) \(\displaystyle MN=4\) и \(\displaystyle \frac{AB+CD}{2}=\frac{2{,}5+5{,}5}{2}=\frac{8}{2}=4{\small,}\) значит,
\(\displaystyle MN=\frac{AB+CD}{2}{\small.}\)
То есть в трапеции \(\displaystyle ABCD\) отрезок \(\displaystyle MN{\small,}\) соединяющий боковые стороны, параллелен основаниям и равен полусумме оснований. Следовательно, \(\displaystyle MN\) – средняя линия трапеции \(\displaystyle ABCD{\small.}\)
Значит, \(\displaystyle N\) – середина стороны \(\displaystyle AD{\small.}\) Тогда
\(\displaystyle ND=\frac{1}{2} \cdot AD=\frac{1}{2} \cdot 7=3{,}5\, \footnotesize м{\small.}\)
Ответ: \(\displaystyle 3{,}5\, \footnotesize м{\small.}\)