Три прямые пересекаются в одной точке, как показано на рисунке.
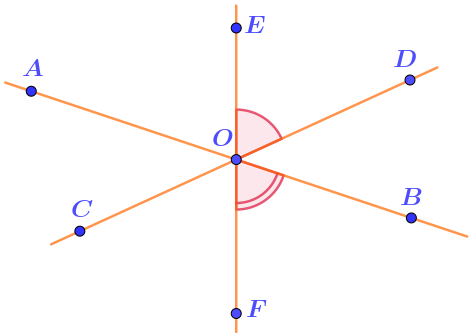
Известны величины отмеченных углов:
\(\displaystyle \angle DOE=65\degree {\small ,\;}\angle BOF=71\degree {\small .}\)
Найти величину угла \(\displaystyle AOC{\small .}\)
\(\displaystyle \angle AOC=\)\(\displaystyle \degree \)
По свойству вертикальных углов, величины этих углов равны:
\(\displaystyle \angle AOC=\angle DOB\)
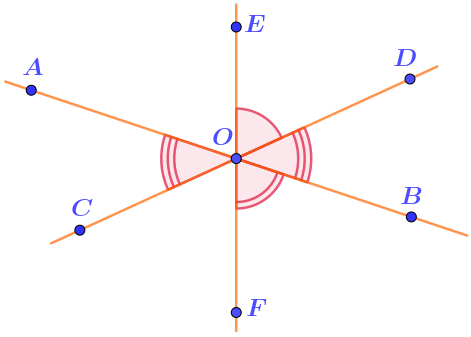
Запишем равенство величины угла, составленного из частей, сумме величин этих частей:
\(\displaystyle \angle EOF= \angle EOD + \angle DOB + \angle BOF\)
Выразим из равенства величину угла \(\displaystyle DOB\) и подставим известные величины остальных углов:
\(\displaystyle \angle DOB=\angle EOF- \angle EOD-\angle BOF=180\degree-65\degree-71\degree=44 \degree {\small .}\)
Ответ: \(\displaystyle 44 \degree {\small .}\)