СПОСОБ \(\displaystyle 1{\small.}\)
Воспользуемся правилом:
Правило Отрезок, соединяющий середины диагоналей трапеции
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности оснований.
| \(\displaystyle \color{red}{m}=\frac{\color{blue}{a}-\color{blue}{b}}{2}\) | 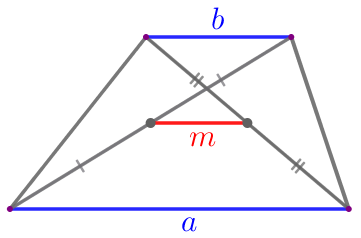 |
По условию основания трапеции равны \(\displaystyle 3\) и \(\displaystyle 7{\small.}\)
Согласно правилу длина отрезка, соединяющего середины диагоналей данной трапеции, равна
\(\displaystyle \frac{7-3}{2}=\frac{4}{2}=2{\small.}\)
Ответ: \(\displaystyle 2{\small.}\)
СПОСОБ \(\displaystyle 2{\small.}\)
Пусть \(\displaystyle ABCD\) – трапеция: - \(\displaystyle BC=3{\small,}\) \(\displaystyle AD=7\) – основания;
- \(\displaystyle AC\) и \(\displaystyle BD\) – диагонали;
- \(\displaystyle L\) – середина \(\displaystyle AC{\small;}\)
- \(\displaystyle P\) – середина \(\displaystyle BD{\small.}\)
Требуется найти длину отрезка \(\displaystyle LP{\small.}\) | 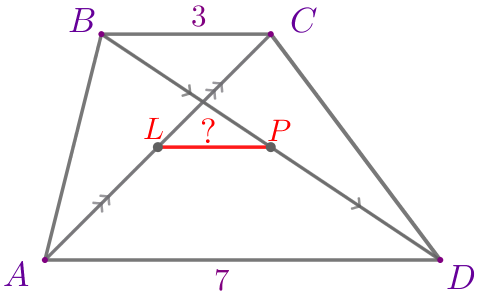 |
Выполним дополнительное построение.
Проведём отрезок \(\displaystyle MN\) – среднюю линию трапеции.
Точки \(\displaystyle L\) и \(\displaystyle P\) лежат на средней линии \(\displaystyle MN\) трапеции \(\displaystyle ABCD{\small.}\)
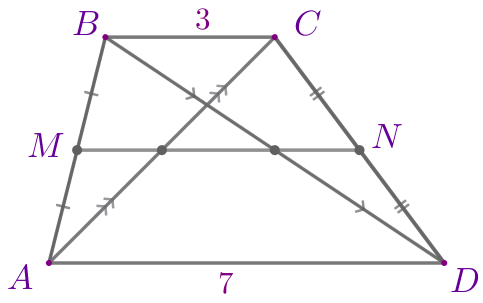 | Так как \(\displaystyle MN\) – средняя линия трапеции \(\displaystyle ABCD{\small,}\) то точки \(\displaystyle M\) и \(\displaystyle N\) – середины сторон \(\displaystyle AB\) и \(\displaystyle CD\) соответственно. По свойству средняя линия параллельна основаниям: \(\displaystyle MN \parallel AD{\small;}\) \(\displaystyle MN \parallel BC{\small.}\) |
Рассмотрим треугольник \(\displaystyle ABD{\small.}\)
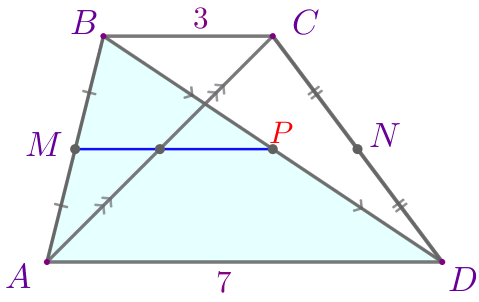 | Точки \(\displaystyle M\) и \(\displaystyle P\) – середины сторон \(\displaystyle AB\) и \(\displaystyle BD{\small.}\) Значит, \(\displaystyle MP\) – средняя линия треугольника \(\displaystyle ABD{\small.}\) По свойству средняя линия параллельна основанию: \(\displaystyle MP \parallel AD{\small.}\) |
Так как \(\displaystyle MN \parallel AD\) и \(\displaystyle MP \parallel AD{\small,}\) то точки \(\displaystyle M{\small,}\) \(\displaystyle N\) и \(\displaystyle P\) лежат на одной прямой.
Рассмотрим треугольник \(\displaystyle ABC{\small.}\)
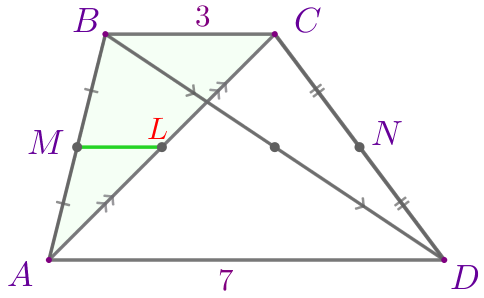 | Точки \(\displaystyle M\) и \(\displaystyle L\) – середины сторон \(\displaystyle AB\) и \(\displaystyle AC{\small.}\) Значит, \(\displaystyle ML\) – средняя линия треугольника \(\displaystyle ABC{\small.}\) По свойству средняя линия параллельна основанию: \(\displaystyle ML \parallel BC{\small.}\) |
Так как \(\displaystyle MN \parallel BC\) и \(\displaystyle ML \parallel BC{\small,}\) то точки \(\displaystyle M{\small,}\) \(\displaystyle N\) и \(\displaystyle L\) лежат на одной прямой.
В результате получаем:
середины диагоналей трапеции лежат на средней линии этой трапеции.
Рассмотрим треугольник \(\displaystyle ABD{\small.}\)
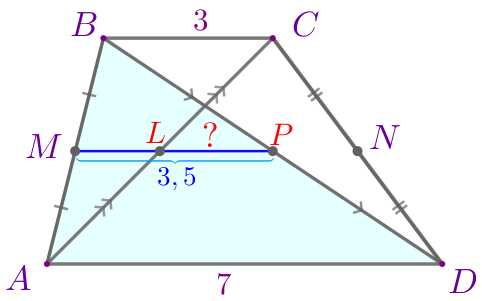 | \(\displaystyle MP\) – средняя линия треугольника \(\displaystyle ABD{\small.}\) По свойству \(\displaystyle MP=\frac{1}{2}\cdot AD=\frac{1}{2}\cdot 7=3{,}5{\small.}\) |
Рассмотрим треугольник \(\displaystyle ABC{\small.}\)
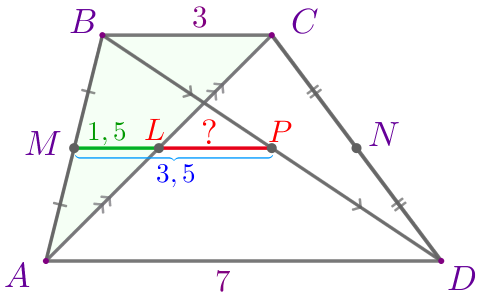 | \(\displaystyle ML\) – средняя линия треугольника \(\displaystyle ABC{\small.}\) По свойству \(\displaystyle ML=\frac{1}{2}\cdot BC=\frac{1}{2}\cdot 3=1{,}5{\small.}\) |
Так как точка \(\displaystyle L\) лежит на отрезке \(\displaystyle MP{\small,}\) то
\(\displaystyle LP=MP-ML=3{,}5-1{,}5=2{\small.}\)
Ответ: \(\displaystyle 2{\small.}\)






