Теория: Отрезок, соединяющий середины диагоналей (короткая версия)

Расстояние от точки до прямой равно длине перпендикуляра, проведённого из этой точки к данной прямой. Пусть:

• \(\displaystyle AC\) – перпендикуляр, проведённый из точки \(\displaystyle A\) к прямой \(\displaystyle l{\small;}\)
• \(\displaystyle BD\) – перпендикуляр, проведённый из точки \(\displaystyle B\) к прямой \(\displaystyle l{\small.}\)

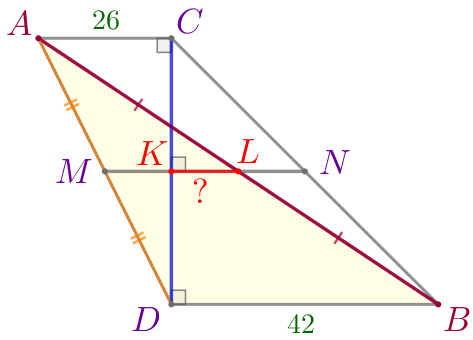
Изобразим предложенную в задаче конструкцию в виде трапеции \(\displaystyle ACBD{\small:}\)

\(\displaystyle AC=26\) – меньшее основание; \(\displaystyle BD=42\) – большее основание; \(\displaystyle L\) – середина отрезка \(\displaystyle AB{\small;}\) \(\displaystyle LK \perp CD{\small.}\) Требуется найти длину \(\displaystyle LK{\small.}\)

Замечание / комментарий

Если две прямые перпендикулярны к третьей, то эти две прямые параллельны: \(\displaystyle \color{darkviolet}{a} \perp \color{green}{c}\)   и   \(\displaystyle \color{darkviolet}{b} \perp \color{green}{c}\) \(\displaystyle \Longrightarrow\) \(\displaystyle \color{darkviolet}{a} \parallel \color{darkviolet}{b}{\small.}\)

Так как прямые \(\displaystyle LK{\small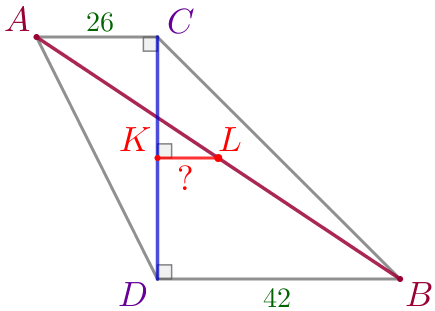,}\) \(\displaystyle AC\) и \(\displaystyle BD\) перпендикулярны \(\displaystyle CD{\small,}\) то

\(\displaystyle LK \parallel AC \parallel BD{\small.}\)

Выполним дополнительное построение.

Продлим отрезок \(\displaystyle LK\) до пересечения с боковыми сторонами трапеции \(\displaystyle ACBD{\small.}\)

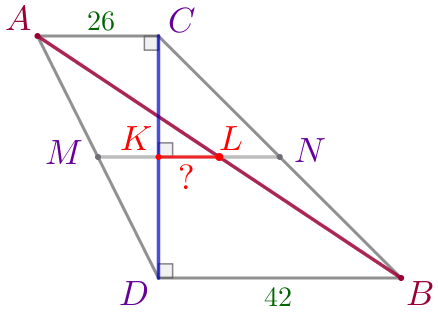Пусть \(\displaystyle M\) – точка пересечения прямой \(\displaystyle LK\) со стороной \(\displaystyle AD{\small;}\) \(\displaystyle N\) – точка пересечения прямой \(\displaystyle LK\) со стороной \(\displaystyle CB{\small.}\)

признак средней линии треугольника

Если отрезок параллелен стороне треугольника, а его концы лежат на сторонах треугольника так, что один из них есть середина стороны, то этот отрезок – средняя линия треугольника.

Рассмотрим треугольник \(\displaystyle ABD{\small.}\)

\(\displaystyle LM \parallel BD{\small;}\) \(\displaystyle L\) – середина \(\displaystyle AB{\small.}\) Следовательно, \(\displaystyle LM\) – средняя линия треугольника \(\displaystyle ABD{\small,}\) значит, \(\displaystyle M\) – середина \(\displaystyle AD{\small.}\)

 

Рассмотрим треугольник \(\displaystyle ABC{\small.}\)

\(\displaystyle LN \parallel AC{\small;}\)  \(\displaystyle L\) – середина \(\displaystyle AB{\small.}\) Следовательно, \(\displaystyle LN\) – средняя линия треугольника \(\displaystyle ABC{\small,}\) значит, \(\displaystyle N\) – середина \(\displaystyle BC{\small.}\)

 

Точки \(\displaystyle M\) и \(\displaystyle N\) – середины боковых сторон трапеции \(\displaystyle ACBD{\small,}\) тогда по определению \(\displaystyle MN\) является средней линией трапеции \(\displaystyle ACBD{\small.}\)

Так как средняя линия делит диагонали трапеции пополам, то \(\displaystyle K\) – середина \(\displaystyle CD{\small.}\)

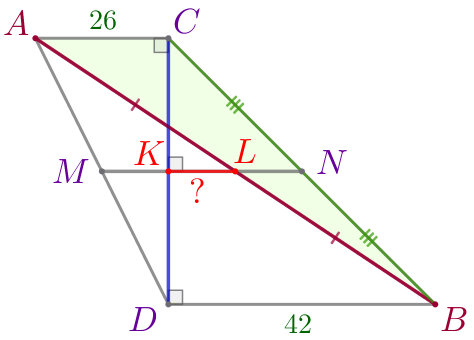
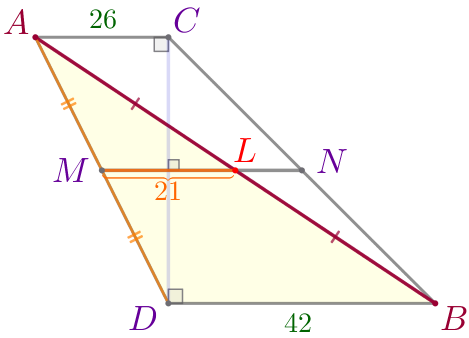\(\displaystyle ML\) – средняя линия треугольника \(\displaystyle ABD{\small.}\) По свойству \(\displaystyle ML=\frac{1}{2}\cdot BD=\frac{1}{2}\cdot 42=21{\small.}\)

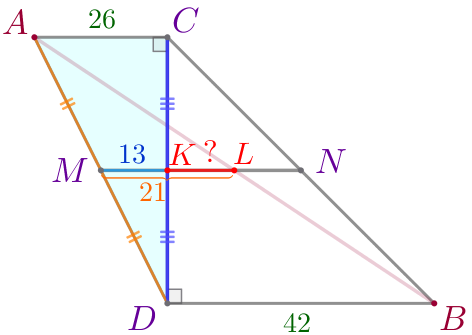\(\displaystyle MK\) – средняя линия треугольника \(\displaystyle ADC{\small.}\) По свойству  \(\displaystyle MK=\frac{1}{2}\cdot AC=\frac{1}{2}\cdot 26=13{\small.}\)

Так как точка \(\displaystyle K\) лежит на отрезке \(\displaystyle ML{\small,}\) то 

\(\displaystyle LK=ML-MK=21-13=8{\small.}\)

Ответ: \(\displaystyle 8{\small.}\)