Skip to main content

Теория: Дополнительные построения (короткая версия)

Задание

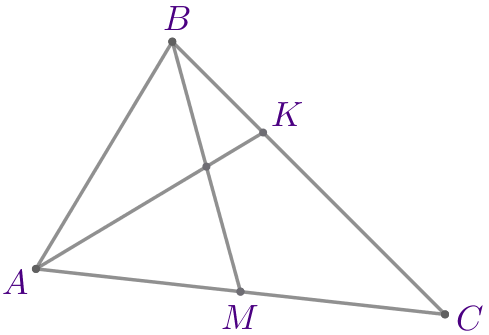
Через вершину \(\displaystyle A\) и середину медианы \(\displaystyle BM\) треугольника \(\displaystyle ABC\) провели прямую. Эта прямая пересекает сторону \(\displaystyle BC\) в точке \(\displaystyle K{\small.}\) Найдите длину отрезка \(\displaystyle BK{\small,}\) если \(\displaystyle BC=27{\small.}\)

\(\displaystyle BK=\)\(\displaystyle {\small.}\)

Решение
  • \(\displaystyle ABC\) – треугольник;
  • \(\displaystyle BC=27{\small;}\)
  • \(\displaystyle BM\) – медиана;
  • \(\displaystyle P\) – середина \(\displaystyle BM{\small;}\)
  • \(\displaystyle K\) – точка пересечения прямой \(\displaystyle AP\) и стороны \(\displaystyle BC{\small.}\)

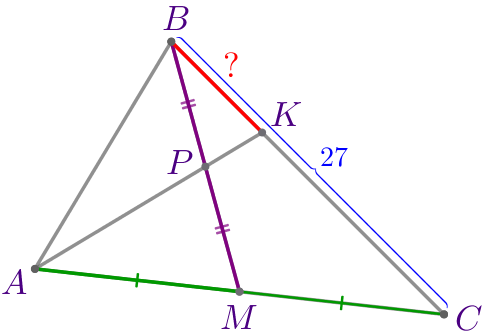Требуется найти длину отрезка \(\displaystyle BK{\small.}\)

 

Выполним дополнительное построение.

Через точку \(\displaystyle M\) параллельно прямой \(\displaystyle AK\) проведём прямую \(\displaystyle MT{\small.}\)

\(\displaystyle T\) – точка пересечения \(\displaystyle MT\) и \(\displaystyle BC{\small.}\)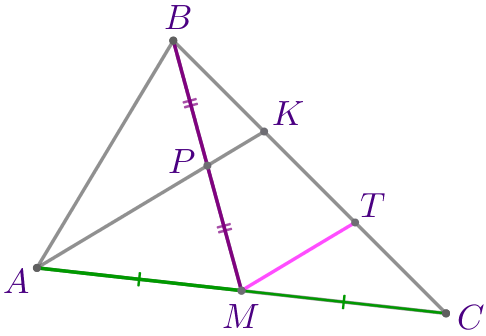

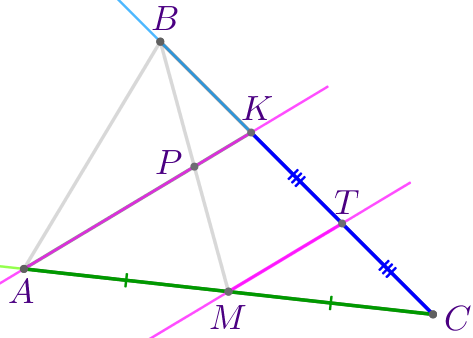Вспомним теорему о пропорциональных отрезках.

\(\displaystyle \color{red}{1{\small.}}\) Cекущие \(\displaystyle CA\) и \(\displaystyle CK\) пересечены параллельными прямыми \(\displaystyle MT\) и \(\displaystyle AK{\small.}\)

Согласно теореме о пропорциональных отрезках:

\(\displaystyle \frac{CT}{CM}=\frac{KT}{AM}{\small.}\)

По условию \(\displaystyle BM\) – медиана треугольника \(\displaystyle ABC{\small,}\) значит,

\(\displaystyle CM=AM{\small.}\)

Следовательно,

\(\displaystyle CT=KT{\small.}\)

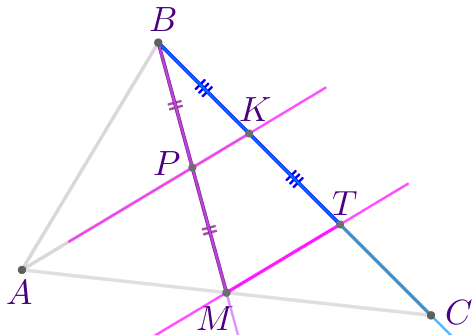\(\displaystyle \color{red}{2{\small.}}\) Cекущие \(\displaystyle BM\) и \(\displaystyle BT\) пересечены параллельными прямыми \(\displaystyle PK\) и \(\displaystyle MT{\small.}\)

Согласно теореме о пропорциональных отрезках:

\(\displaystyle \frac{BK}{BP}=\frac{KT}{PM}{\small.}\)

По условию \(\displaystyle P\) – середина отрезка \(\displaystyle BM{\small,}\) значит,

\(\displaystyle BP=PM{\small.}\)

Следовательно,

\(\displaystyle BK=KT{\small.}\)

В результате получаем:

\(\displaystyle BK=KT=CT\)

и

\(\displaystyle BK+KT+CT=BC{\small.}\)

Значит,

\(\displaystyle BK=\frac{1}{3}\cdot BC{\small.}\)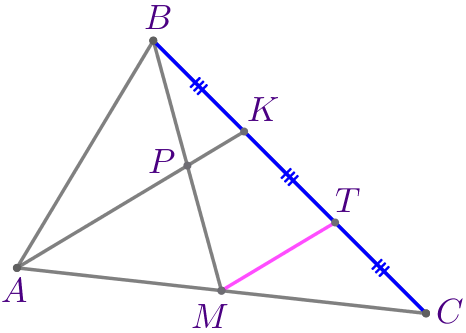

Подставим \(\displaystyle BC=27{\small:}\)

\(\displaystyle BK=\frac{1}{3}\cdot 27=9{\small.}\)

Ответ: \(\displaystyle BK=9{\small.}\)