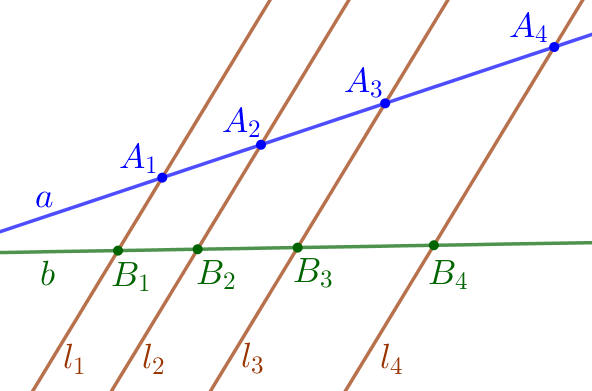
Точки \(\displaystyle M\) и \(\displaystyle K\) делят стороны \(\displaystyle AB\) и \(\displaystyle BC\) треугольника \(\displaystyle ABC\) в отношении \(\displaystyle 3:4\) и \(\displaystyle 5:2\) соответственно, считая от их общей вершины \(\displaystyle B{\small.}\) Медиана \(\displaystyle BL\) треугольника \(\displaystyle ABC\) пересекает отрезок \(\displaystyle MK\) в точке \(\displaystyle P{\small.}\) Найдите \(\displaystyle MP:PK{\small.}\)
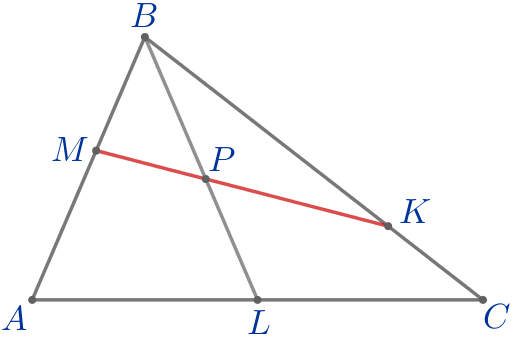
\(\displaystyle MP:PK=\)\(\displaystyle :\)\(\displaystyle {\small.}\)
\(\displaystyle ABC\) – треугольник:
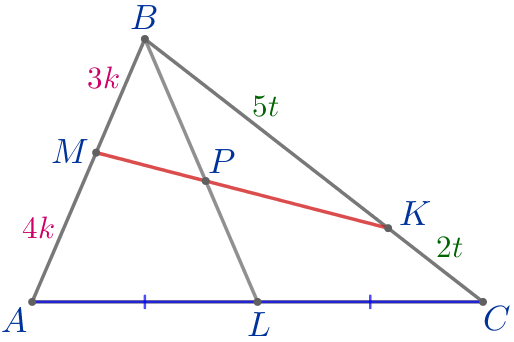 |
\(\displaystyle BM=3k{\small,}\) \(\displaystyle AM=4k{\small;}\)
\(\displaystyle BK=5t{\small,}\) \(\displaystyle CK=2t{\small;}\)
|
Требуется найти \(\displaystyle MP:PK=\large \color{red}{?}\)
Выполним дополнительное построение. Через точки \(\displaystyle M\) и \(\displaystyle K\) параллельно медиане \(\displaystyle BL\) проведём прямые \(\displaystyle MN\) и \(\displaystyle KF{\small.}\) \(\displaystyle N\) – точка пересечения \(\displaystyle MN\) и \(\displaystyle AC{\small.}\) \(\displaystyle F\) – точка пересечения \(\displaystyle KF\) и \(\displaystyle AC{\small.}\) | 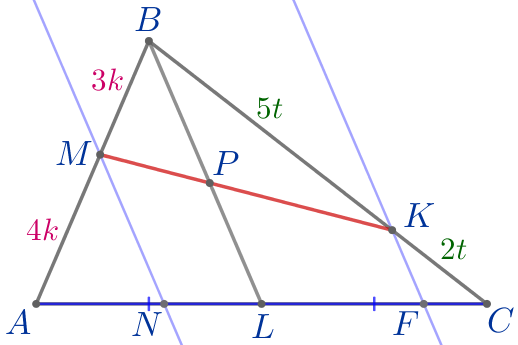 |
Секущие \(\displaystyle MK\) и \(\displaystyle NF\) пересечены параллельными прямыми \(\displaystyle MN{\small,}\) \(\displaystyle PL\) и \(\displaystyle KF{\small.}\)
Согласно теореме о пропорциональных отрезках:
\(\displaystyle \frac{MP}{NL}=\frac{PK}{LF}{\small.}\)
По свойству пропорции получаем:
\(\displaystyle MP:PK=NL:LF{\small.}\)
Найдём отношение длин отрезков \(\displaystyle NL\) и \(\displaystyle LF{\small.}\)
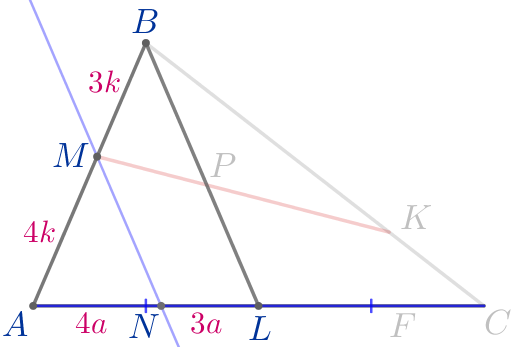 | Согласно теореме о пропорциональных отрезках: \(\displaystyle \frac{AN}{AM}=\frac{NL}{BM}{\small.}\) По свойству пропорции получаем: \(\displaystyle AN:NL=AM:BM=4:3{\small.}\) То есть \(\displaystyle AN=4a{\small,}\) \(\displaystyle NL=3a{\small,}\) \(\displaystyle AL=7a{\small.}\) |
Следовательно,
\(\displaystyle NL=\frac{3}{7} \cdot AL{\small.}\)
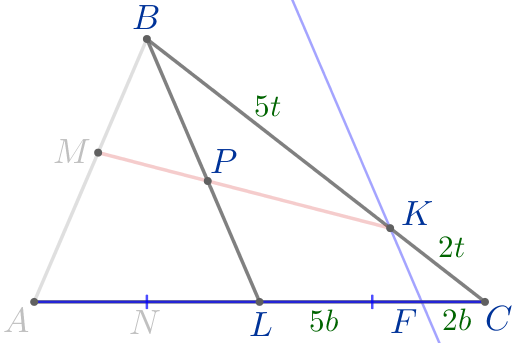 | Согласно теореме о пропорциональных отрезках: \(\displaystyle \frac{CF}{CK}=\frac{LF}{BK}{\small.}\) По свойству пропорции получаем: \(\displaystyle CF:LF=CK:BK=2:5{\small.}\) То есть \(\displaystyle CF=2b{\small,}\) \(\displaystyle LF=5b{\small,}\) \(\displaystyle CL=7b{\small.}\) |
Следовательно,
\(\displaystyle LF=\frac{5}{7} \cdot CL{\small.}\)
В результате получаем
\(\displaystyle NL:LF=\left(\frac{3}{7}\cdot AL\right):\left(\frac{5}{7}\cdot CL\right){\small.}\)
Так как \(\displaystyle AL=CL{\small,}\) то
\(\displaystyle NL:LF=\left(\frac{3}{7} \cdot CL\right):\left(\frac{5}{7} \cdot CL\right)=\frac{3}{7} :\frac{5}{7}=\frac{3}{7} \cdot \frac{7}{5}=\frac{3}{5}=3:5{\small.}\)
Значит,
\(\displaystyle MP:PK=3:5{\small.}\)
Ответ: \(\displaystyle MP:PK=3:5{\small.}\)