На клетчатой бумаге изображён многоугольник.
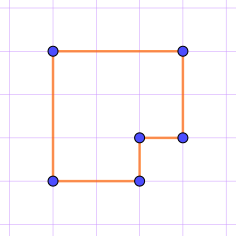
Найдите его периметр (в миллиметрах), если длина стороны клетки равна одному сантиметру.
\(\displaystyle {\footnotesize мм}\)
В рассматриваемом многоугольнике шесть сторон.
Чтобы не ошибиться, выберем одну из вершин, например, в левом нижнем углу рисунка.
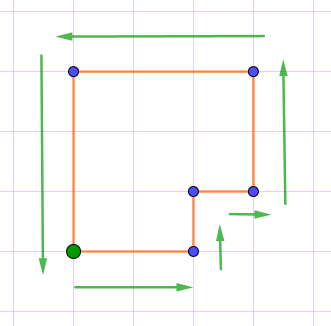
Двигаясь против часовой стрелки по контуру многоугольника, сосчитаем клетки вдоль каждой из сторон, пока не вернёмся в исходнрую вершину:
\(\displaystyle P=2+1+1+2+3+3=12~({\footnotesize клеток}){\small .}\)
Сторона клетки, по условию, равна одному сантиметру.
В одном сантиметре десять миллиметров.
Значит, для получения ответа следует умножить число клеток на \(\displaystyle 10{\small:}\)
\(\displaystyle P=12\cdot 10=120~({\footnotesize мм}){\small .}\)
Ответ: \(\displaystyle 120\,{\footnotesize мм}{\small .}\)