Задание
На клетчатой бумаге изображён многоугольник, периметр которого равен \(\displaystyle 12\) сантиметрам.
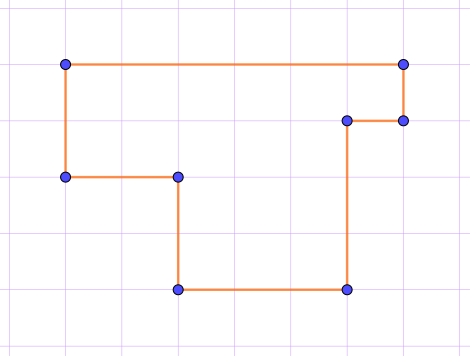
Какова длина стороны клетки в миллиметрах?
\(\displaystyle {\footnotesize мм} {\small .}\)
Решение
Найдём периметр многоугольника, выраженный в клетках.
Для этого сложим длины всех сторон или заменим многоугольник на прямоугольник того же периметра.
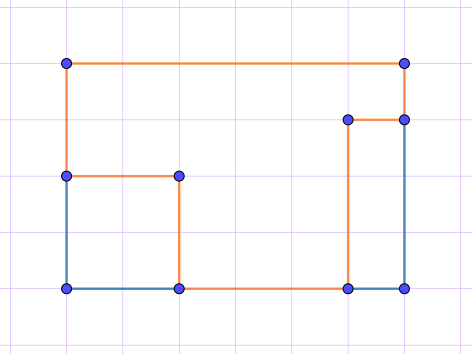
Обоими способами получаем \(\displaystyle 20\) клеток:
\(\displaystyle P=3+3+1+1+6+2+2+2=20~({\footnotesize клеток})\)
или
\(\displaystyle P=2\cdot (6+4)=20~({\footnotesize клеток})\)
Чтобы найти длину \(\displaystyle d\) стороны клетки, разделим данное значение периметра в сантиметрах на найденное значение в клетках.
\(\displaystyle d=\frac{12}{20}=0{,}6~({\footnotesize см})\)
Ответ требуется дать в миллиметрах.
В одном сантиметре десять миллиметров.
Поэтому
\(\displaystyle d=0{,}6\cdot 10=6~({\footnotesize мм})\)
Ответ: \(\displaystyle 6\,{\footnotesize мм}{\small .}\)