На клетчатой бумаге изображён многоугольник.
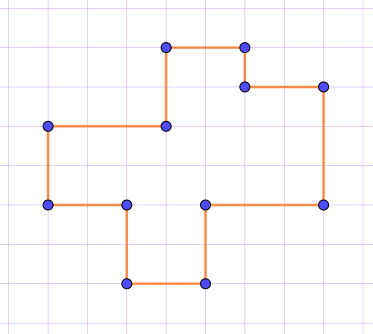
Найдите его периметр (в сантиметрах), если длина стороны клетки равна двум сантиметрам.
\(\displaystyle {\footnotesize см}\)
У многоугольника довольно много сторон \(\displaystyle -\) двенадцать.
Можно просто сложить их длины, но есть возможность упростить вычисления.
Достроим многоугольник до прямоугольника, "выворачивая" некоторые из прямых углов.
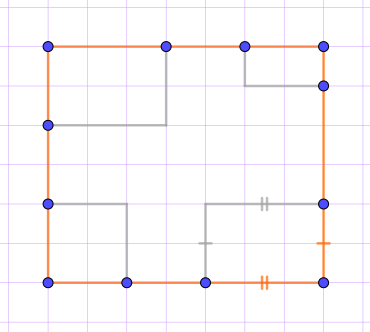
При этом периметр многоугольника останется прежним.
В правом нижнем углу рисунка показано, что стирая две стороны многоугольника, мы заменяем их на пару равных им отрезков.
Благодаря этому приёму, можем воспользоваться формулой периметра прямоугольника. Сложим длины смежных сторон и удвоим сумму:
\(\displaystyle P=2\cdot(6+7)=26~({\footnotesize клеток}){\small .}\)
Длина стороны клетки известна и равна \(\displaystyle 2\,{\footnotesize см} {\small .}\)
Значит, периметр фигуры равен
\(\displaystyle P=26 \cdot2 = 52\,({\footnotesize см}){\small .}\)
Ответ: \(\displaystyle 52\,{\footnotesize см}{\small .}\)