В треугольнике \(\displaystyle ABC\) чевианы \(\displaystyle AK,\,BL\) и \(\displaystyle CM\) пересекаются в одной точке. Прямые \(\displaystyle KL\) и \(\displaystyle AB\) пересекаются в точке \(\displaystyle E\small.\) Найдите \(\displaystyle AE\small,\) если \(\displaystyle AM=1,\,BM=3\small.\)
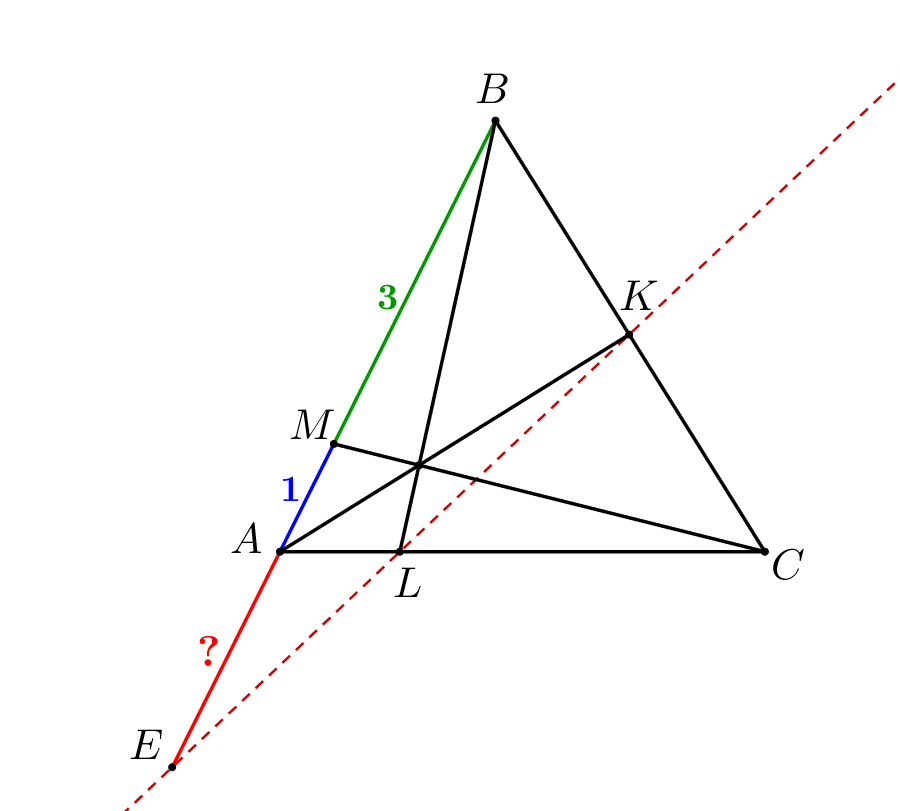
Чтобы решить задачу:
- найдем произведение некоторых отношений, используя теорему Чевы;
- найдем \(\displaystyle AE\) по тереме Менелая.
\(\displaystyle \frac{BK}{CK}\cdot\frac{CL}{AL}=3\small.\)
Отрезки \(\displaystyle AK,\,BL\) и \(\displaystyle CM\) пересекаются в одной точке. Тогда по теореме Чевы: \(\displaystyle \frac{\color{blue}{AM}}{\color{red}{BM}}\cdot\frac{\color{blue}{BK}}{\color{red}{CK}}\cdot\frac{\color{blue}{CL}}{\color{red}{AL}}=1\small.\)
\(\displaystyle \frac{1}{3}\cdot\frac{BK}{CK}\cdot\frac{CL}{AL}=1\small,\) \(\displaystyle \frac{BK}{CK}\cdot\frac{CL}{AL}=3\small.\) | 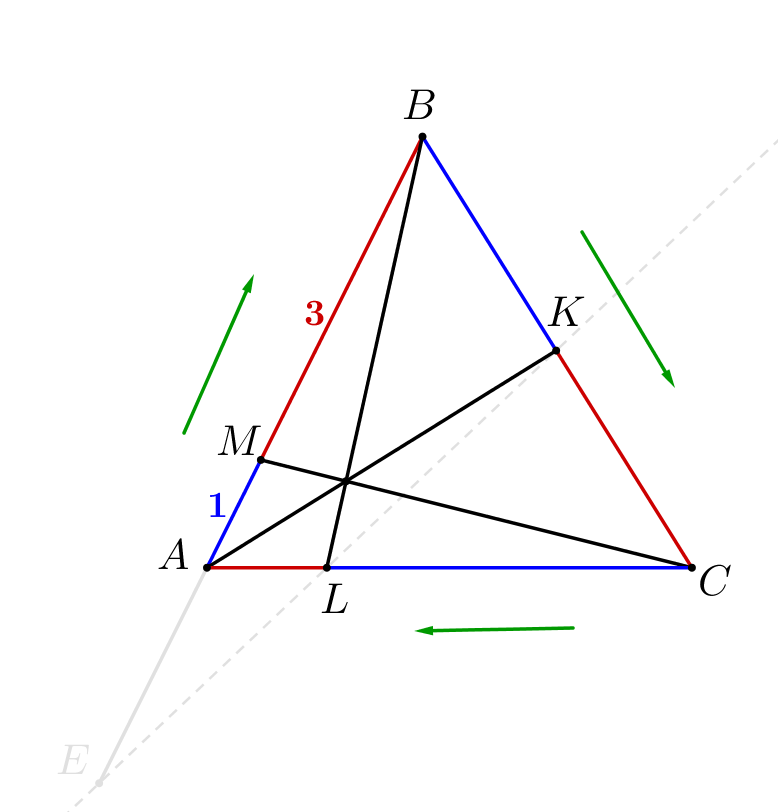 |
\(\displaystyle \frac{AE}{BE}=\frac{1}{3}\small.\)
Точки \(\displaystyle K,\,L\) и \(\displaystyle E\) лежат на одной прямой. Тогда по теореме Менелая: \(\displaystyle \frac{\color{blue}{BK}}{\color{red}{CK}}\cdot\frac{\color{blue}{CL}}{\color{red}{AL}}\cdot\frac{\color{blue}{AE}}{\color{red}{BE}}=1\small.\) Подставим \(\displaystyle \color{green}{\frac{BK}{CK}\cdot\frac{CL}{AL}=3}\small.\) Получаем: \(\displaystyle \color{green}{3}\cdot\frac{AE}{BE}=1\small,\) \(\displaystyle \frac{AE}{BE}=\frac{1}{3}\small.\) | 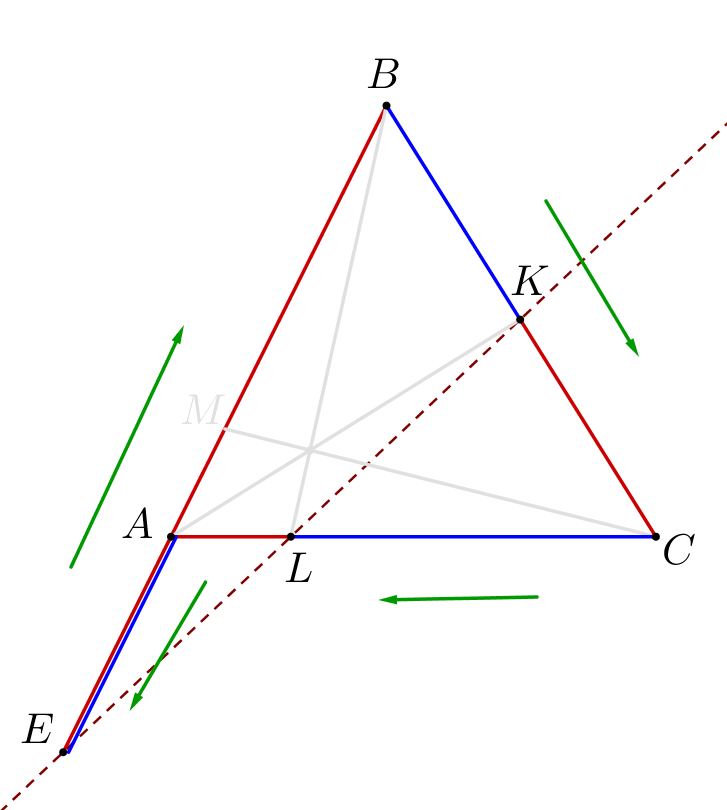 |
То есть \(\displaystyle BE=3AE\small.\)
Обозначим \(\displaystyle AE\) за \(\displaystyle x\small,\) тогда
- \(\displaystyle AE=x\small,\)
- \(\displaystyle BE=AB+AE=4+x\small.\)
Значит,
\(\displaystyle 4+x=BE=3AE=3x\small.\)
Решая уравнение, находим \(\displaystyle x{\small:}\)
\(\displaystyle 2x=4\) и \(\displaystyle x=2\small.\)
Ответ: \(\displaystyle AE=2\small.\)