На тетрадном листе изображён план участка с огородом.
На участке расположена бытовка, к которой от калитки проложена дорожка. Если идти по ней от калитки, то слева окажутся несколько одинаковых грядок прямоугольной формы. Справа \(\displaystyle -\) парник, длина которого на \(\displaystyle 270\;{\footnotesize см}\) больше ширины, и три яблони. Рядом с бытовкой оборудовано пространство для отдыха под открытым небом, и высажены кусты смородины.
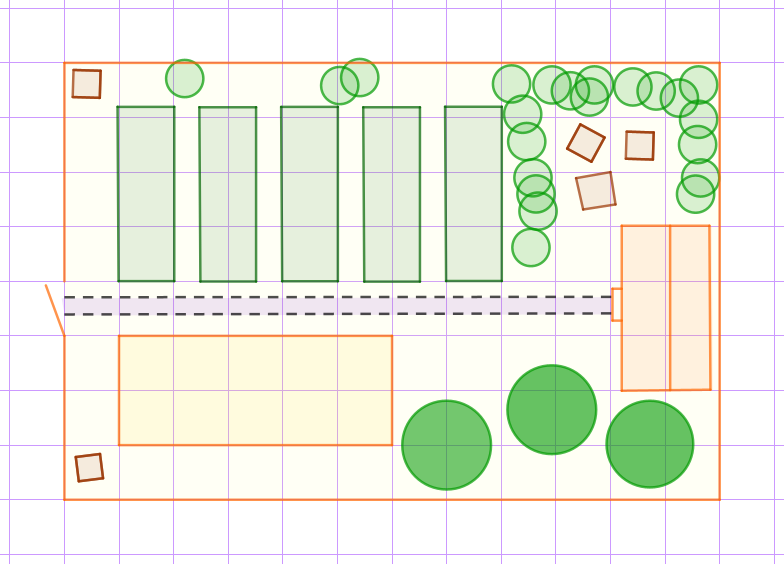
Каково расстояние (в метрах) от калитки до бытовки?
м
Изображения длины и ширины парника составляют соответственно пять и две клетки. Таким образом, изображение длины на \(\displaystyle 5-2=3\) клетки длиннее изображения ширины.
По условию, длина больше ширины на \(\displaystyle 270\) сантиметров. Разделив эту величину на три клетки, узнаем расстояние, которое соответствует длине стороны клетки: \(\displaystyle \frac{270}{3}=90~{\footnotesize см}{\small .}\)
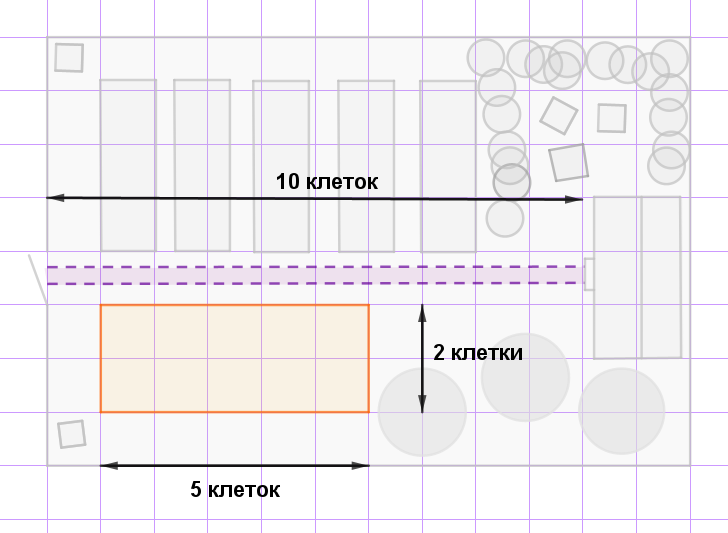
Изображение дорожки составляет \(\displaystyle 10\) клеток.
Сторона клетки соответствует \(\displaystyle 90\) сантиметрам.
Значит, искомое расстояние равно \(\displaystyle 10\cdot90 = 900~{\footnotesize см}\) или \(\displaystyle 9~{\footnotesize м}{\small .}\)
Ответ: \(\displaystyle 9\) метров.