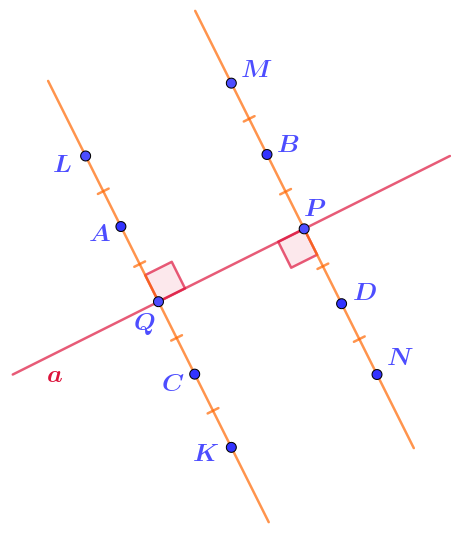
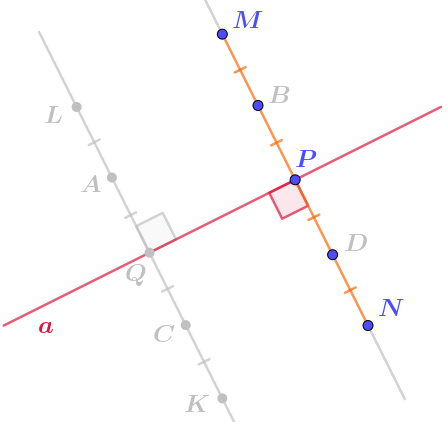
Через точки \(\displaystyle P\) и \(\displaystyle Q\) прямой \(\displaystyle a\) проведены две перпендикулярные ей прямые.
На них взяты несколько точек так, что образовались отмеченные равные отрезки.
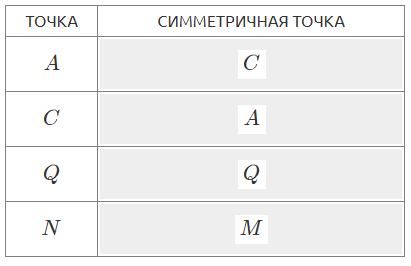
Дополните пары симметричных относительно прямой \(\displaystyle a\) точек.
| ТОЧКА | СИММЕТРИЧНАЯ ТОЧКА |
| \(\displaystyle A\) | |
| \(\displaystyle C\) | |
| \(\displaystyle Q\) | |
| \(\displaystyle N\) |
Две точки, не принадлежащие прямой, симметричны друг другу относительно этой прямой, если:
- прямая проходит через середину отрезка, соединяющего эти точки;
- прямая перпендикулярна этому отрезку.
Каждая точка, принадлежащая прямой, считается симметричной самой себе относительно этой прямой.
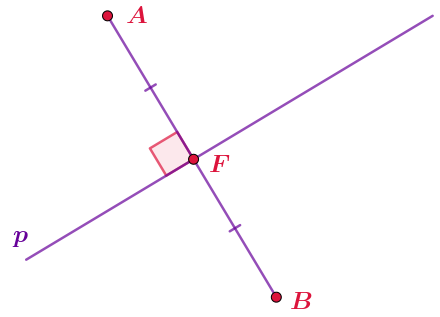
На рисунке точки \(\displaystyle A\) и \(\displaystyle B\) симметричны относительно прямой \(\displaystyle p{\small .}\) Середина \(\displaystyle F\) отрезка \(\displaystyle AB\) симметрична сама себе относительно этой прямой.
Пусть точка \(\displaystyle A \) не принадлежит прямой \(\displaystyle p{ \small .}\)
Чтобы найти точку \(\displaystyle B{\small ,}\) симметричную точке \(\displaystyle A\) относительно прямой \(\displaystyle p{ \small :}\)
- через точку \(\displaystyle A\) проводят прямую, перпендикулярную прямой \(\displaystyle p\,{\small ;}\)
- от точки \(\displaystyle F\) пересечения прямых откладывают отрезок \(\displaystyle FB{\small ,}\) равный отрезку \(\displaystyle FA{\small ,}\) но расположенный по другую сторону прямой \(\displaystyle p{\small .}\)
Точка \(\displaystyle Q\) – середина отрезка \(\displaystyle AC{\small .}\)
Прямая \(\displaystyle a\) перпендикулярна отрезку \(\displaystyle AC{\small .}\)
Значит, точки \(\displaystyle A\) и \(\displaystyle C\) симметричны друг другу относительно прямой \(\displaystyle a{\small .}\)
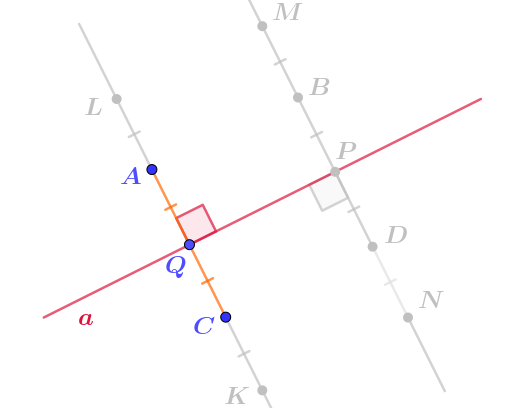
Точка \(\displaystyle Q\) принадлежит прямой \(\displaystyle a{\small .}\) Значит, она симметрична сама себе относительно этой прямой.
Точка \(\displaystyle P\) – середина отрезка \(\displaystyle MN{\small ,}\) так как отрезки \(\displaystyle PM\) и \(\displaystyle PN\) составлены из равных частей.
Прямая \(\displaystyle a\) перпендикулярна отрезку \(\displaystyle MN{\small .}\)
Значит, точки \(\displaystyle N\) и \(\displaystyle M\) симметричны относительно прямой \(\displaystyle a{\small .}\)
Ответ: