Все изображённые фигуры имеют разное количество осей симметрии.
Сопоставьте каждой фигуре число её осей симметрии.
| ФИГУРА | КОЛИЧЕСТВО ОСЕЙ СИММЕТРИИ |
 | |
 | |
 | |
 | |
 |
В условии утверждается, что все рассматриваемые фигуры имеют разное число осей симметрии.
Поэтому решить задачу можно, если последовательно отыскать фигуры имеющие как минимум четыре, три две, одну ось симметрии.
Фигура называется симметричной относительно прямой, если точки, симметричные точкам фигуры относительно этой прямой, образуют ту же фигуру. Саму прямую, при этом, называют осью симметрии фигуры.
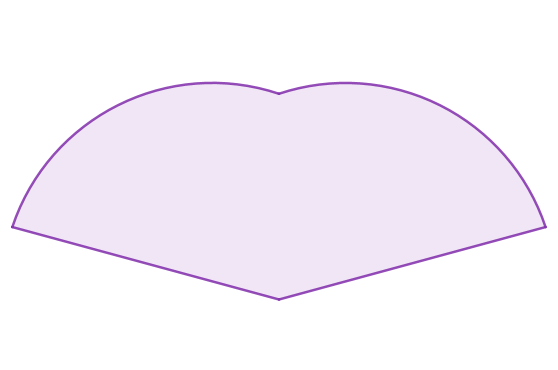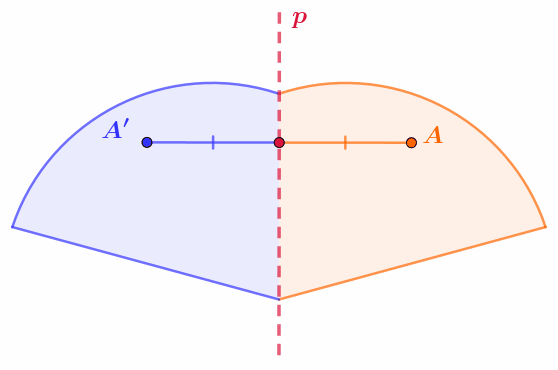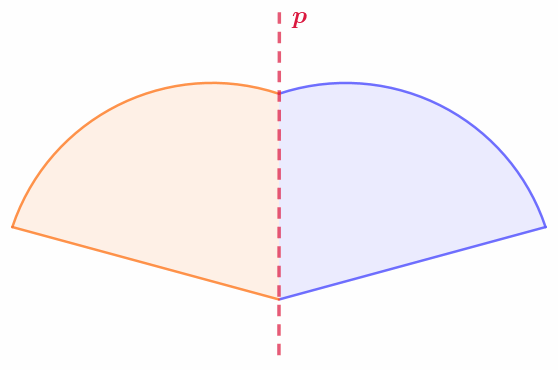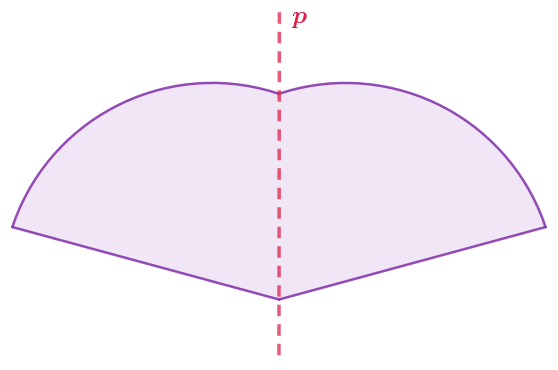
У отрезка ровно две оси симметрии:
| 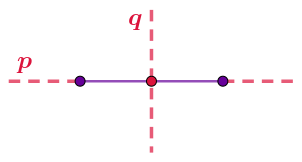 |
| У неразвёрнутого угла одна ось симметрии \(\displaystyle -\) прямая, содержащая его биссектрису. | 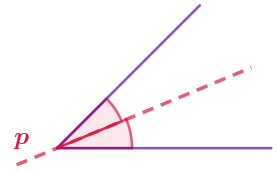 |
| У равнобедренного треугольника осью симметрии является прямая, содержащая его медиану (биссектрису, высоту), проведённую к основанию. | 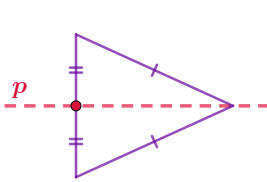 |
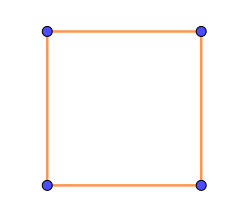
На рисунке показаны:
- две перпендикулярные друг другу прямые, разделяющие квадрат на два равнобедренных треугольника;
- два перпендикуляра к парам сторон квадрата, проходящие через середины этих его сторон.
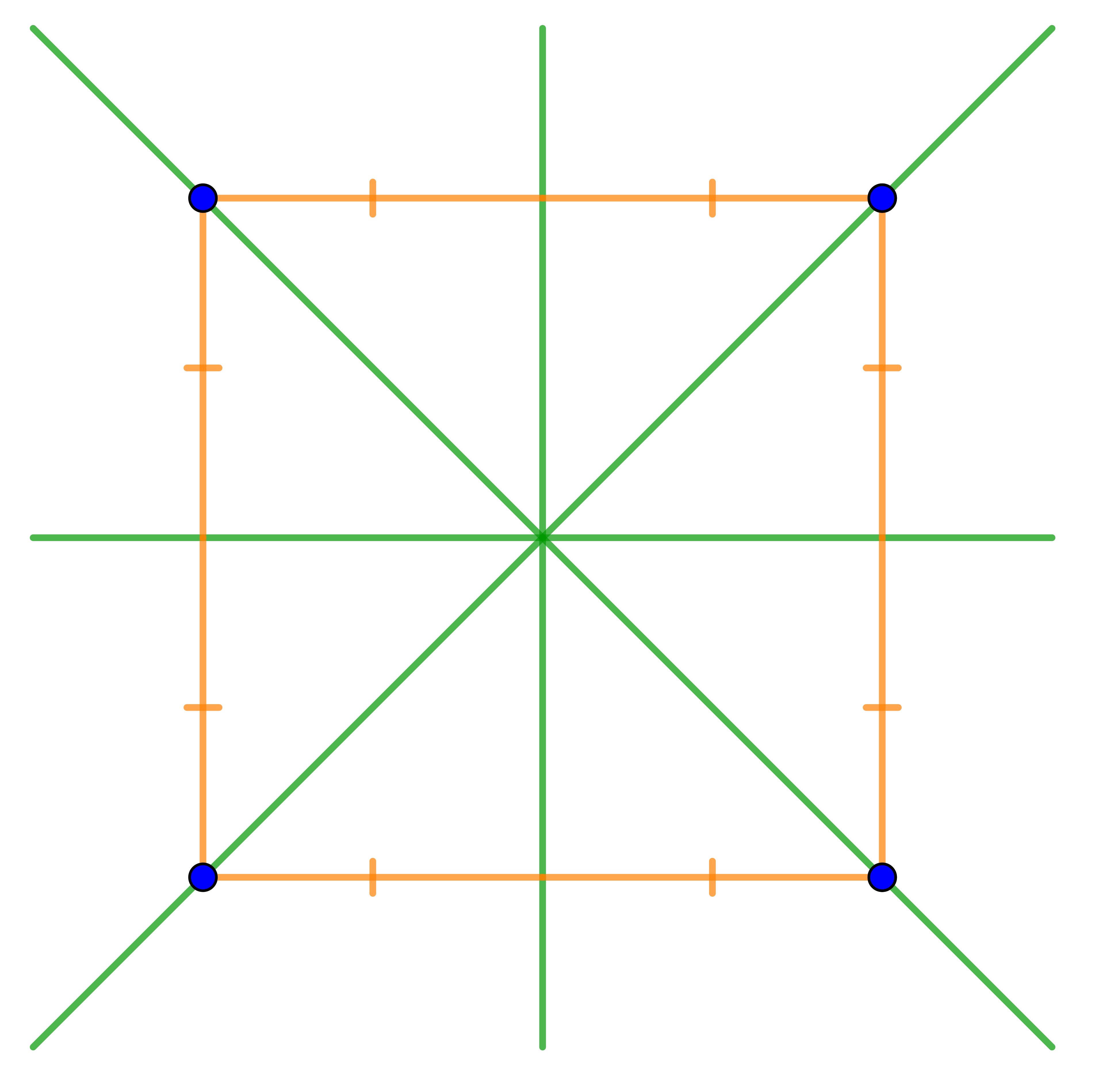
Возможность провести эти прямые обеспечивается свойствами квадрата.
То, что они являются осями симметрии квадрата, следует из того, что они являются осями симметрии отрезков и равнобедренных треугольников рисунка.
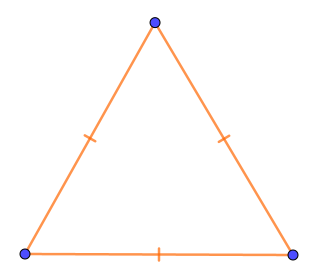
Проведём прямые, содержащие медианы (а тем самым и высоты) равностороннего треугольника.
Каждая из них является осью симметрии треугольника по свойствам равнобедренного треугольника.
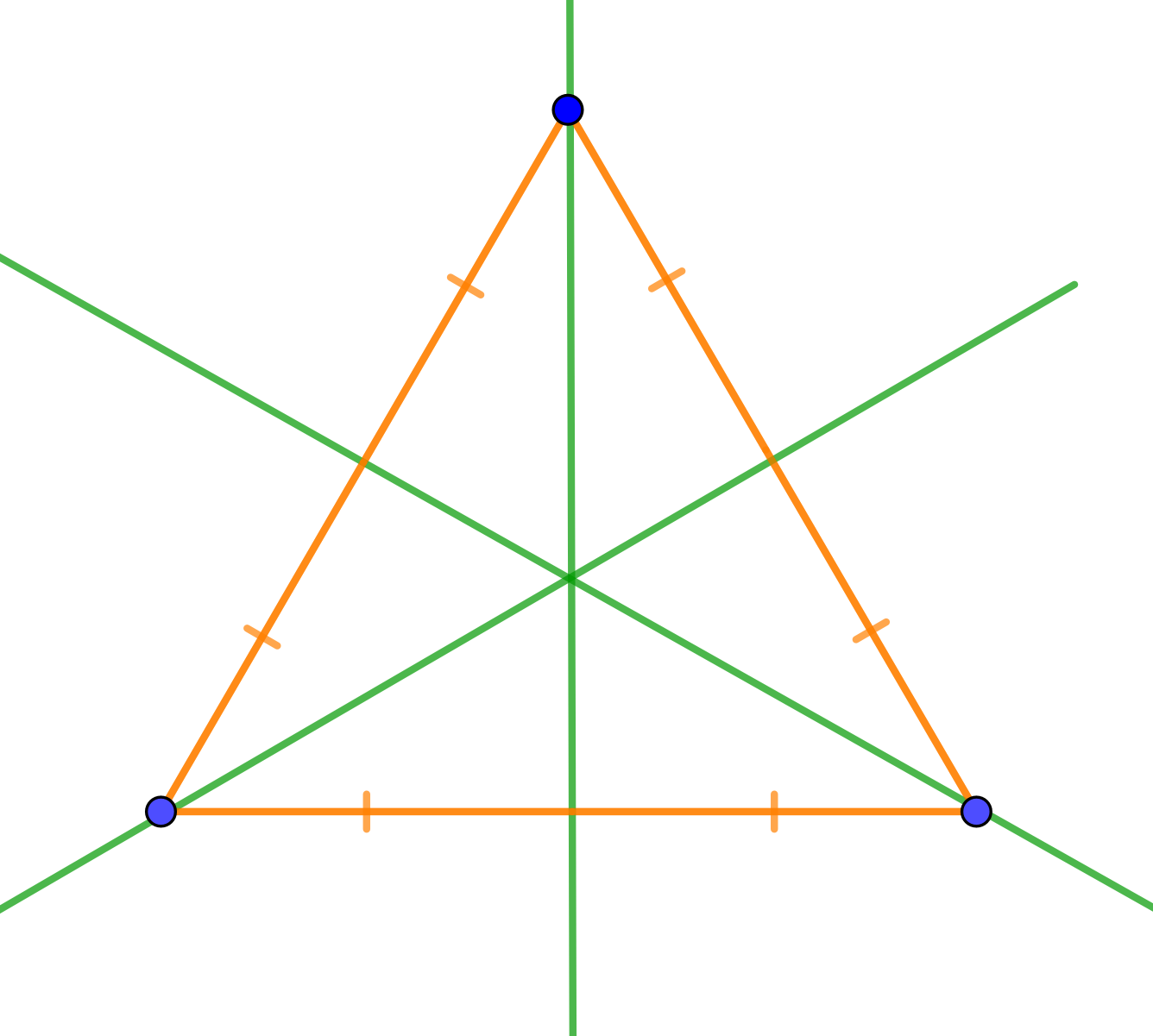
То и другое \(\displaystyle -\) известные свойства симметричных фигур.
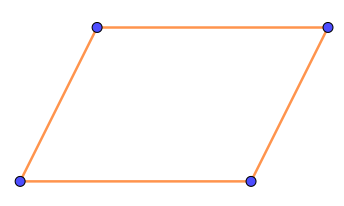
Для данного четырёхугольника действительно не удаётся найти прямую, претендующую на роль оси симметрии.
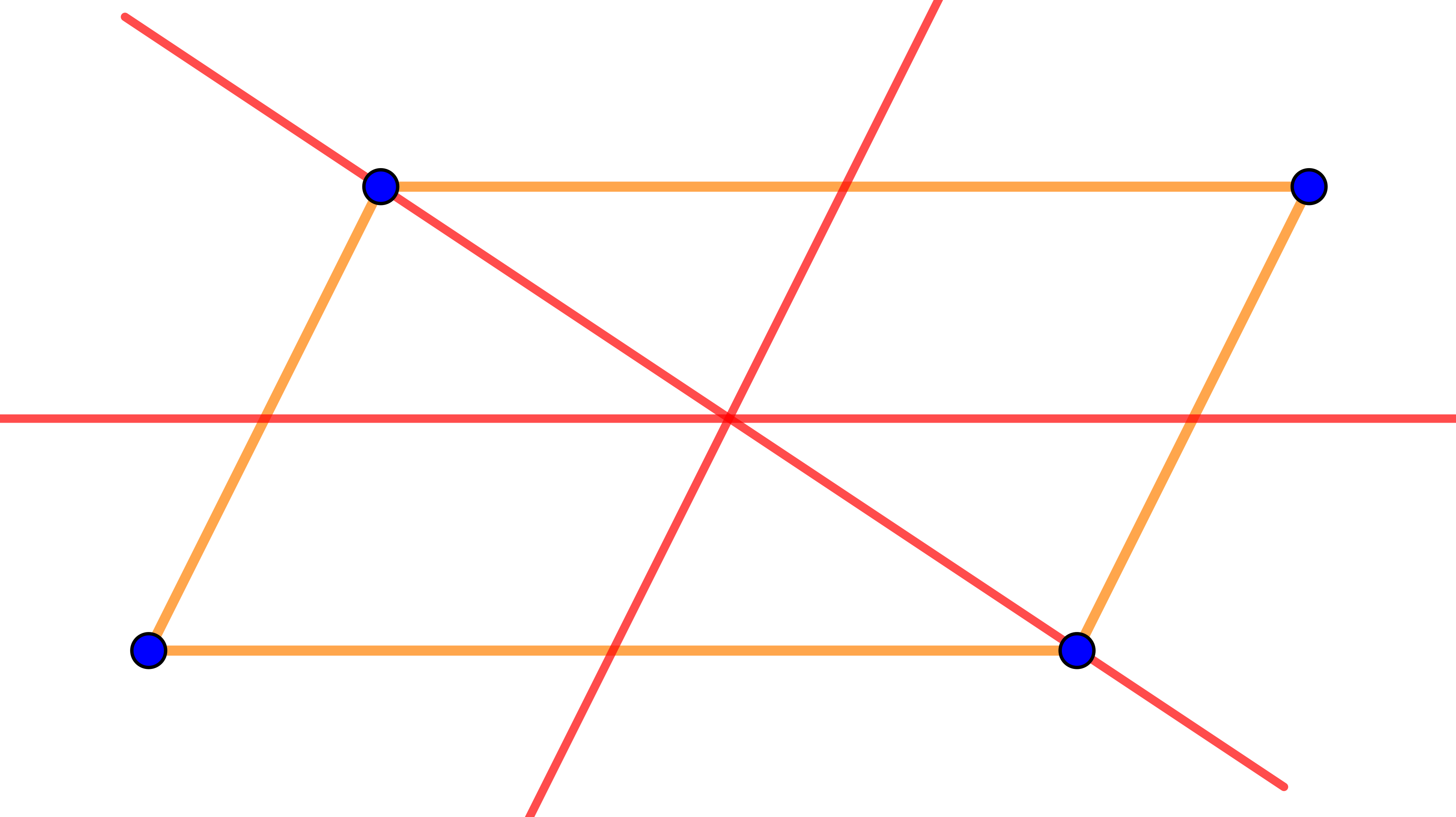
Это добавляет уверенности в правильности решения.
| Ответ: | 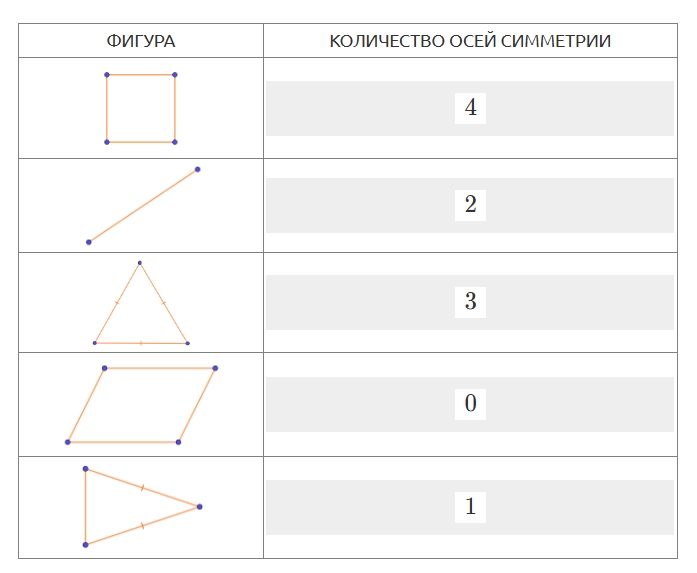 |