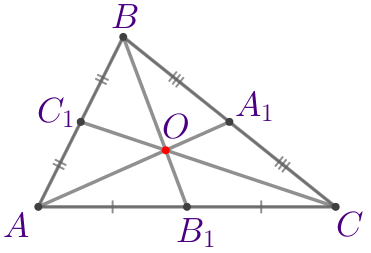
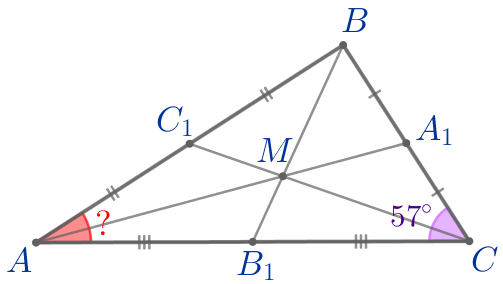
Медианы \(\displaystyle AA_1{\small,}\) \(\displaystyle BB_1\) и \(\displaystyle CC_1\) треугольника \(\displaystyle ABC\) пересекаются в точке \(\displaystyle M{\small.}\) Найдите величину угла \(\displaystyle BAC{\small,}\) если известно, что \(\displaystyle \angle ACB=57^{\circ}\) и \(\displaystyle AC=3BM{\small.}\)
\(\displaystyle \angle BAC=\)\(\displaystyle ^{\circ}{\small.}\)
\(\displaystyle ABC\) – треугольник.
 |
|
Требуется найти угол \(\displaystyle BAC{\small.}\)
| Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении \(\displaystyle 2:1{\small,}\) считая от вершины. | |
| \(\displaystyle \frac{AO}{OA_1}=\frac{BO}{OB_1}=\frac{CO}{OC_1}=\frac{2}{1}\) |
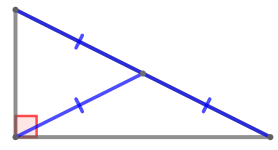
Согласно теореме медиана \(\displaystyle BB_1\) составляет три равных части, а отрезок \(\displaystyle BM\) – две таких части. Следовательно,
\(\displaystyle BB_1=\frac{3 BM}{2}{\small.}\)
По условию \(\displaystyle AC=3BM{\small,}\) значит,
\(\displaystyle BB_1=\frac{3 BM}{2}=\frac{AC}{2}{\small.}\)
То есть медиана \(\displaystyle BB_1\) равна половине стороны, к которой проведена. Следовательно,
\(\displaystyle \triangle ABC\) – прямоугольный,
\(\displaystyle \angle B=90^{\circ}{\small.}\)
Сумма острых углов прямоугольного треугольника равна \(\displaystyle 90^{\circ}{\small.}\)
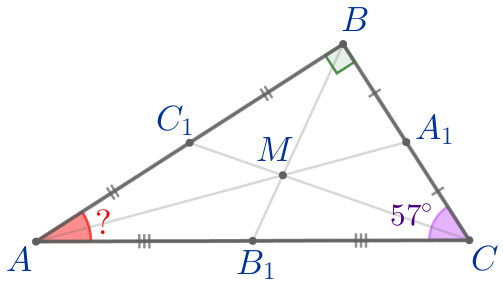 | Значит, \(\displaystyle \angle BAC+\angle ACB=90^{\circ}{\small.}\) Тогда \(\displaystyle \angle BAC=90^{\circ}-\angle ACB{\small;}\) \(\displaystyle \angle BAC=90^{\circ}-57^{\circ}=33^{\circ}{\small.}\) |
Ответ: \(\displaystyle \angle BAC=33^{\circ}{\small.}\)