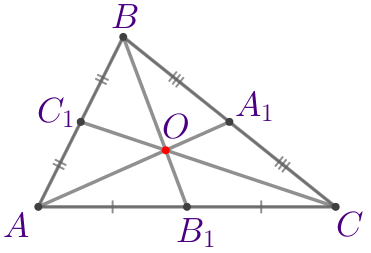
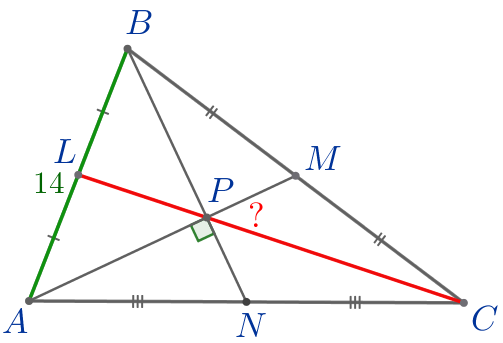
В треугольнике \(\displaystyle ABC\) точки \(\displaystyle L{\small,}\) \(\displaystyle M\) и \(\displaystyle N\) являются серединами сторон \(\displaystyle AB{\small,}\) \(\displaystyle BC\) и \(\displaystyle AC\) соответственно. Отрезки \(\displaystyle AM\) и \(\displaystyle BN\) перпендикулярны и пересекаются в точке \(\displaystyle P{\small.}\) Найдите длину \(\displaystyle CL{\small,}\) если \(\displaystyle AB=14{\small.}\)
\(\displaystyle CL=\)
 | \(\displaystyle ABC\) – треугольник:
Требуется найти длину медианы \(\displaystyle CL{\small.}\) |
\(\displaystyle \frac{CP}{PL}=\frac{2}{1}{\small.}\)
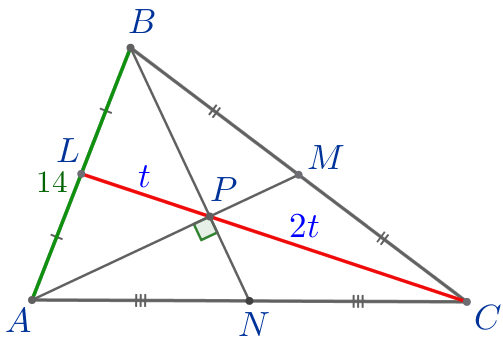 | Пусть \(\displaystyle CP=2t{\small,}\) \(\displaystyle PL=t{\small.}\) Тогда \(\displaystyle CL=CP+PL=2t+t=3t{\small.}\) То есть \(\displaystyle CL=3 \cdot PL{\small.}\) |
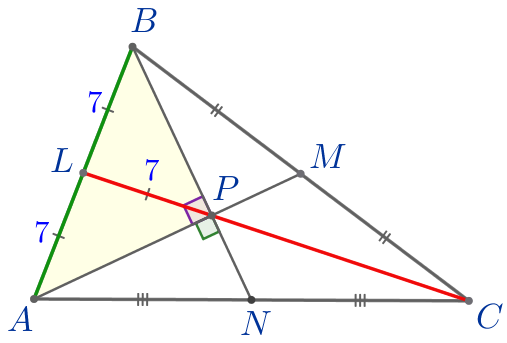 |
\(\displaystyle \triangle APB\) – прямоугольный.
\(\displaystyle PL\) – медиана прямоугольного треугольника \(\displaystyle APB{\small,}\) проведённая к гипотенузе \(\displaystyle AB{\small.}\) |
| Медиана, проведённая к гипотенузе прямоугольного треугольника, равна половине гипотенузы. |
|
Следовательно,
\(\displaystyle PL= \frac{1}{2} \cdot AB=\frac{1}{2} \cdot 14=7{\small.}\)
В результате получаем:
\(\displaystyle CL=3 \cdot PL=3 \cdot 7=21{\small.}\)
Ответ: \(\displaystyle CL=21{\small.}\)