На биссектрисе угла \(\displaystyle A\) треугольника \(\displaystyle ABC\) отметили точку \(\displaystyle O\small.\) При этом оказалось, что \(\displaystyle \angle OCA=\angle OBC=30^{\circ}\) и \(\displaystyle \angle OCB=45^{\circ}\small.\) Найдите синус угла \(\displaystyle OBA\small.\)
В треугольнике \(\displaystyle ABC\small{:}\)
Точка \(\displaystyle O\) лежит на биссектрисе угла \(\displaystyle A\small,\) значит \(\displaystyle \angle CAO=\angle BAO=\alpha\small.\) | 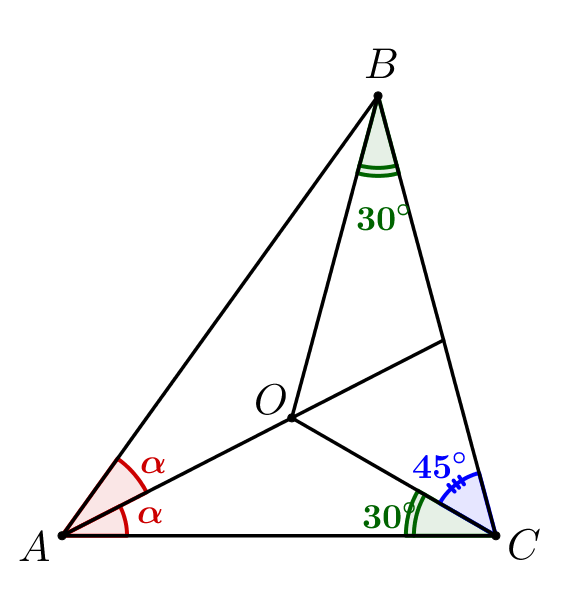 |
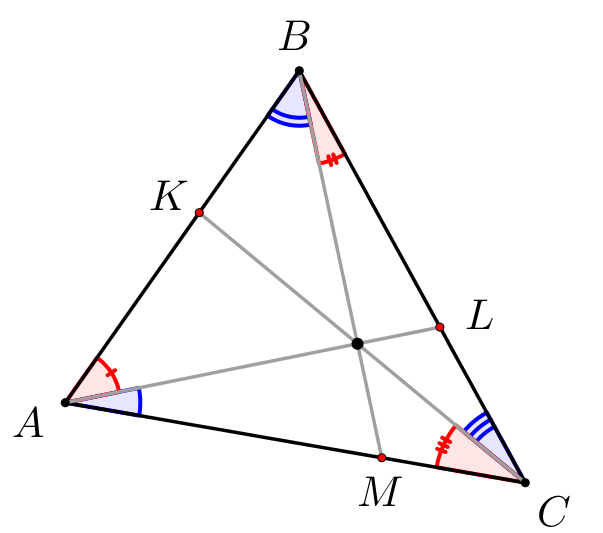
Продлим отрезки \(\displaystyle AO,\,BO\) и \(\displaystyle CO\) до пересечениями со сторонами. Получились три чевианы, пересекающиеся в одной точке. Некоторые из углов, на которые чевианы делят углы треугольника, нам известны.
Тогда напишем теорему Чевы в синусах для треугольника \(\displaystyle ABC\) и чевиан \(\displaystyle AO,\,BO\) и \(\displaystyle CO{\small:}\) \(\displaystyle \frac{\sin45^{\circ}}{\sin30^{\circ}}\cdot\frac{\sin\alpha}{\sin\alpha}\cdot\frac{\sin\angle OBA}{\sin30^{\circ}}=1\small.\) Сократим \(\displaystyle \sin\alpha\) и подставим известные значения \(\displaystyle \sin30^{\circ}=\frac{1}{2}\) и \(\displaystyle \sin45^{\circ}=\frac{\sqrt{2}}{2}{\small:}\) \(\displaystyle \frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}\cdot\frac{\sin\angle OBA}{\frac{1}{2}}=1\small,\) \(\displaystyle \sin\angle OBA=\frac{1}{4}:\frac{\sqrt2}{2}=\frac{\sqrt2}{4}\small.\) | 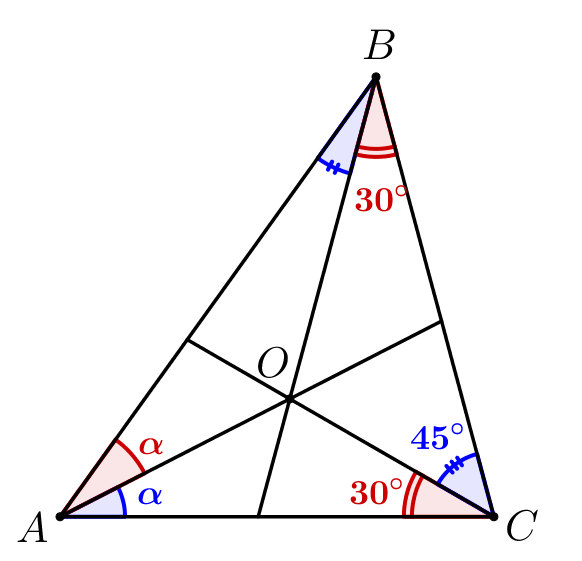 |
Ответ: \(\displaystyle \sin\angle OBA=\frac{\sqrt2}{4}\small.\)