В треугольнике \(\displaystyle ABC\) стороны \(\displaystyle AB\) и \(\displaystyle AC\) равны. На биссектрисе угла \(\displaystyle C\) выбрали точку \(\displaystyle D\) так, что \(\displaystyle \angle DBC=30^{\circ}\) и \(\displaystyle \angle DBA=45^{\circ}\small.\) Прямая \(\displaystyle AD\) пересекает сторону \(\displaystyle BC\) в точке \(\displaystyle E\small.\) Найдите отношение
В треугольнике \(\displaystyle ABC\small{:}\)
Точка \(\displaystyle D\) лежит на биссектрисе угла \(\displaystyle C\small,\) значит \(\displaystyle \angle ACG=\angle BCG=\alpha\small.\) | 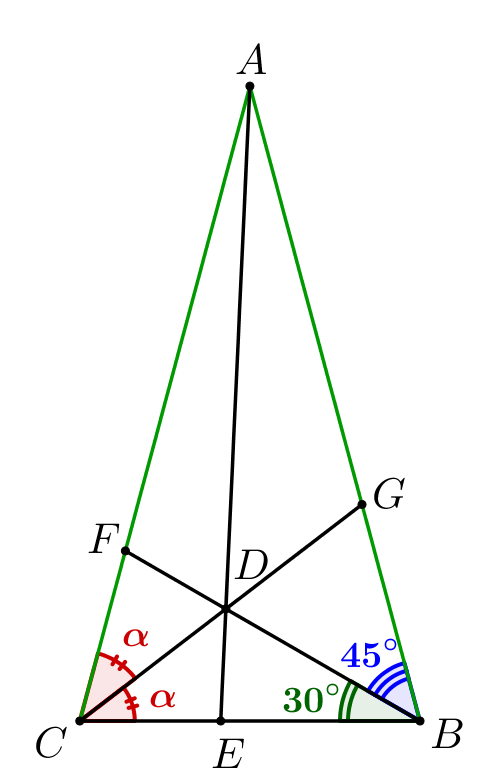 |
Чтобы решить задачу:
- выразим отношение \(\displaystyle BE\) и \(\displaystyle CE\) через синусы углов \(\displaystyle BAE\) и \(\displaystyle CAE\small,\)
- найдем отношение синусов.
\(\displaystyle BE:EC=\frac{\sin \angle BAE}{\sin \angle CAE}\small.\)
По теореме синусов для треугольника \(\displaystyle AEB\small,\) получаем:
\(\displaystyle \frac{AE}{\sin \angle ABE}=\frac{BE}{\sin \angle BAE}\small.\)
По теореме синусов для треугольника \(\displaystyle AEC\small{,}\) получаем:
\(\displaystyle \frac{AE}{\sin \angle ACE}=\frac{CE}{\sin \angle CAE}\small.\)
По условию \(\displaystyle AB=AC\small.\) Треугольник \(\displaystyle ABC\) равнобедренный, значит \(\displaystyle \angle ABC=\angle ACB\small.\)
Тогда левые части теорем синусов равны:
\(\displaystyle \frac{BE}{\sin \angle BAE}=\frac{AE}{\sin \angle ABE}=\frac{AE}{\sin \angle ACE}=\frac{CE}{\sin \angle CAE}\small.\)
Тогда
\(\displaystyle \frac{BE}{CE}=\frac{\sin \angle BAE}{\sin \angle CAE}\small.\)
\(\displaystyle \frac{\sin \angle BAE}{\sin \angle CAE}=\sqrt2\small.\)
В треугольнике \(\displaystyle ABC\) известны углы, на которые чевианы \(\displaystyle CG\) и \(\displaystyle BF\) делят углы треугольника. Тогда можно найти отношение синусов углов, на которые \(\displaystyle AE\) делит угол \(\displaystyle A\small.\)
\(\displaystyle \frac{\color{blue}{\sin \angle BCG}}{\color{red}{\sin \angle GCA}}\cdot\frac{\color{blue}{\sin \angle CAE}}{\color{red}{\sin \angle BAE}}\cdot\frac{\color{blue}{\sin \angle ABF}}{\color{red}{\sin \angle FBC}}=1\small.\)
\(\displaystyle \frac{\cancel{\sin \alpha}}{\cancel{\sin \alpha}}\cdot\frac{{\sin \angle CAE}}{{\sin \angle BAE}}\cdot\frac{{\sin 45^{\circ}}}{{\sin 30^{\circ}}}=1\small,\) \(\displaystyle \frac{\sin \angle BAE}{\sin \angle CAE}=\frac{\sin45^\circ}{\sin30^\circ}=\sqrt2\small.\) | 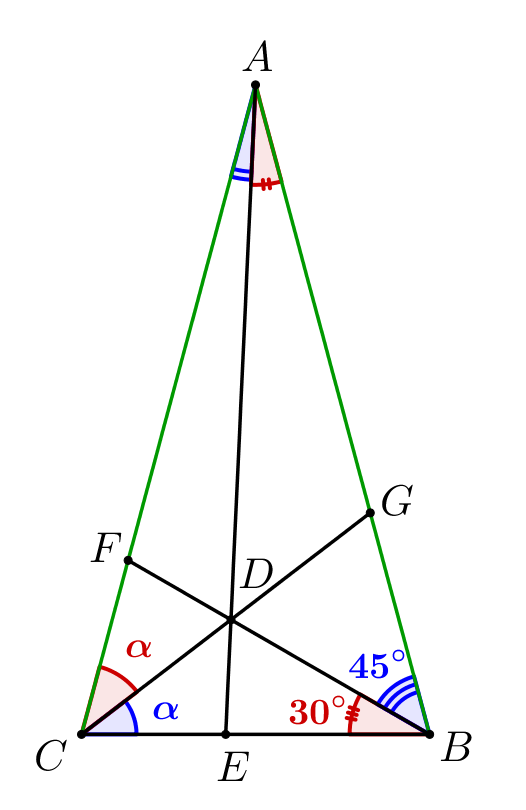 |
Таким образом, получаем:
\(\displaystyle \frac{BE}{EC}=\frac{\sin \angle BAE}{\sin \angle CAE}=\sqrt2\small.\)
Ответ: \(\displaystyle \frac{BE}{EC}=\sqrt2\small.\)