Центры двух окружностей радиусов \(\displaystyle 3\) и \(\displaystyle 5\) находятся на расстоянии \(\displaystyle 10\small.\) Найдите длину отрезка внутренней касательной.
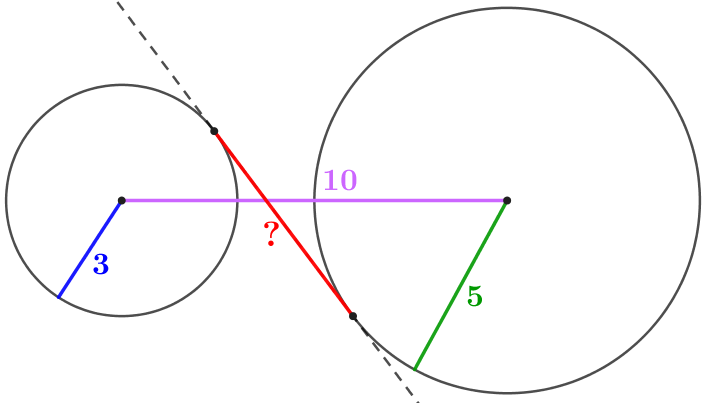
Обозначим центры окружностей буквами \(\displaystyle O\) и \(\displaystyle E{\small,}\) а точки касания общей касательной с окружностями буквами \(\displaystyle X\) и \(\displaystyle Y\) соответственно.
Проведём радиусы \(\displaystyle OX\) и \(\displaystyle EY{\small.}\) Радиус, проведённый в точку касания, перпендикулярен касательной:
| 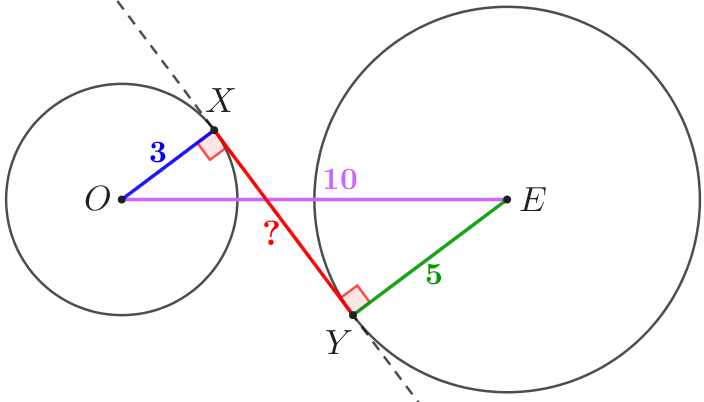 |
Выполним дополнительное построение.
Из точки \(\displaystyle E\) проведём перпендикуляр \(\displaystyle EK\) к продолжению отрезка \(\displaystyle OX{\small.}\)
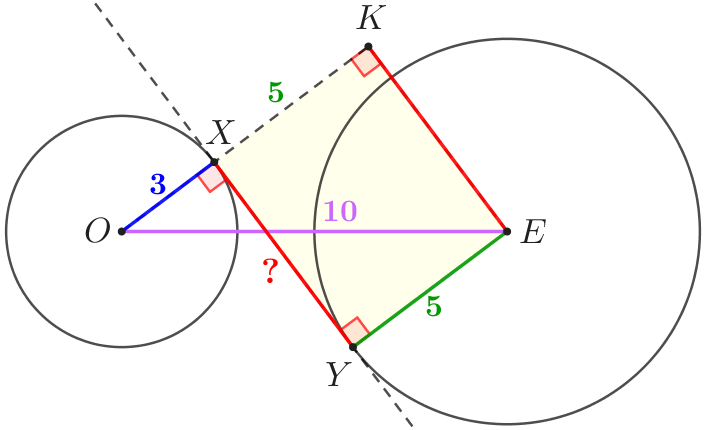 | В четырёхугольнике \(\displaystyle XKEY\) три угла прямые, значит, \(\displaystyle XKEY\) – прямоугольник. В прямоугольнике противоположные стороны равны, то есть
|
Найдем длину \(\displaystyle OK{\small:}\)
\(\displaystyle OK=OX+XK=3+5=8{\small.}\)
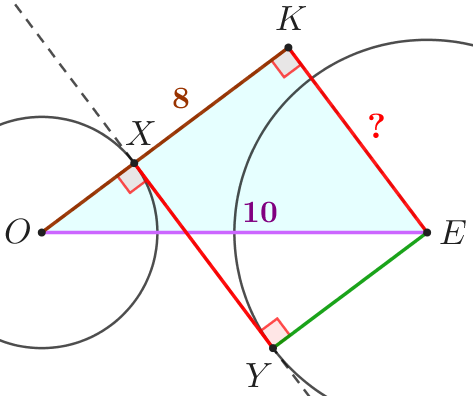 |
По теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: \(\displaystyle OE^2=OK^2+KE^2\small.\) |
Найдем \(\displaystyle KE{\small:}\)
\(\displaystyle KE^2=OE^2-OK^2=10^2-8^2=36{\small,}\)
\(\displaystyle KE=\sqrt{36}=6{\small.}\)
То есть
\(\displaystyle \color{red}{XY}=\color{red}{KE}=6{\small.}\)
Ответ: \(\displaystyle 6{\small.}\)