Задание
Два катета прямоугольного треугольника равны \(\displaystyle 4\) и \(\displaystyle 10 {\small.}\) Найдите площадь этого треугольника.
Решение
Пусть в прямоугольном треугольнике \(\displaystyle ABC\) \(\displaystyle \angle B=90^{\circ} {\small,}\) \(\displaystyle AB=10 {\small,}\) \(\displaystyle BC=4 {\small.}\)
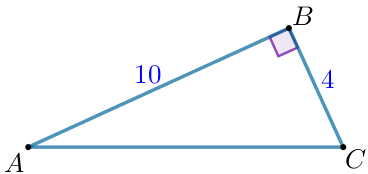 | Площадь прямоугольного треугольника равна половине произведения длин катетов: \(\displaystyle S_{\triangle ABC}= \frac{1}{2}\cdot AB \cdot BC {\small.} \) Тогда \(\displaystyle S_{\triangle ABC}= \frac{1}{2}\cdot 10\cdot 4=20{\small.} \) |
Ответ: \(\displaystyle 20 {\small.}\)