Задание
Сторона треугольника равна \(\displaystyle 16 {\small,}\) а высота, проведённая к этой стороне, равна \(\displaystyle 19 {\small.}\) Найдите площадь этого треугольника.
Решение
Правило
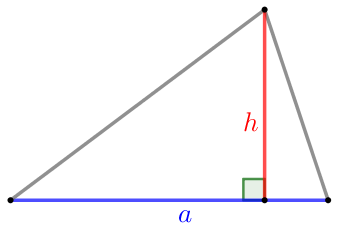
Формула площади треугольника
\(\displaystyle S=\frac{1}{2}\cdot{\color{red}{h}\cdot \color{blue}{a}}\)
|
|
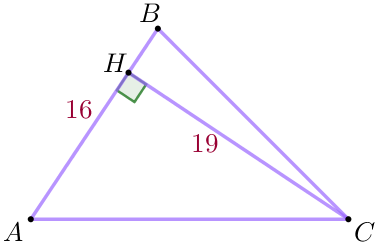 | Пусть в треугольнике \(\displaystyle ABC\) сторона \(\displaystyle AB=16 {\small,}\) \(\displaystyle CH=19\) – высота, проведённая к стороне \(\displaystyle AB {\small.}\) По формуле площади треугольника получаем: \(\displaystyle S_{\triangle ABC}=\frac{1}{2}\cdot CH \cdot AB {\small,}\) \(\displaystyle S_{\triangle ABC}=\frac{1}{2}\cdot 19 \cdot 16=152{\small.}\) |
Ответ: \(\displaystyle 152 {\small.}\)