Графиком линейного уравнения с двумя переменными \(\displaystyle ax+by=c{\small,}\) в котором \(\displaystyle a=0{\small,}\) \(\displaystyle b\ \cancel = \ 0{\small,}\) является прямая, параллельная оси абсцисс, пересекающая ось ординат в точке \(\displaystyle \bigg(0;\frac{c}{b}\bigg){\small.}\) Такое уравнение можно записать короче: \(\displaystyle by=c\) или \(\displaystyle y=\frac{c}{b}{\small.}\) | 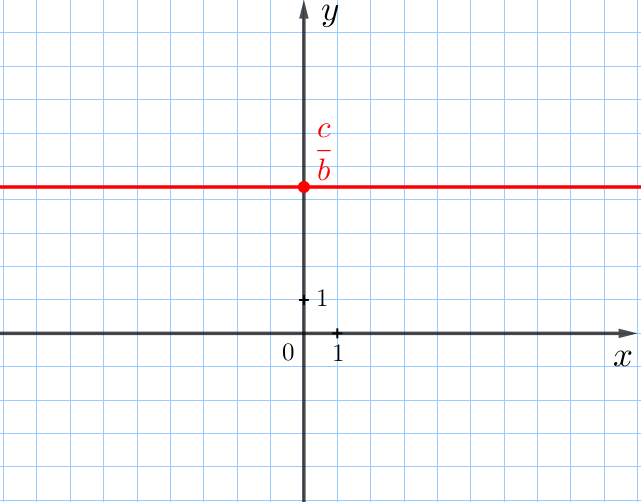 |
Графиком линейного уравнения с двумя переменными \(\displaystyle ax+by=c{\small,}\) в котором \(\displaystyle a\ \cancel=\ 0{\small,}\) \(\displaystyle b\ = \ 0{\small,}\) является прямая, параллельная оси ординат, пересекающая ось абсцисс в точке \(\displaystyle \bigg(\frac{c}{a};0\bigg){\small.}\) Такое уравнение можно записать короче: \(\displaystyle ax=c\) или \(\displaystyle x=\frac{c}{a}{\small.}\) | 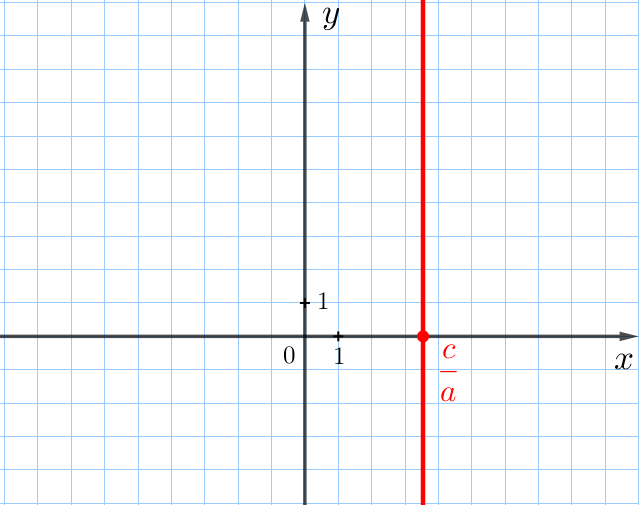 |
Уравнение \(\displaystyle ax+by=c{\small,}\) в котором оба коэффициента при переменных равны нулю, имеет вид
\(\displaystyle 0x+0y=c{\small.}\)
- при \(\displaystyle c=0\) любая пара чисел является решением этого уравнения, а вся координатная плоскость – его графиком;
- при \(\displaystyle c\ \cancel=\ 0\) уравнение не имеет решений, и его график не содержит ни одной точки.