Задание
Укажите промежутки возрастания и убывания функции \(\displaystyle y=|x|{\small .}\)
| функция возрастает на промежутке | |
| функция убывает на промежутке |
Решение
Информация
- Функция возрастает, если большему значению аргумента соответствует большее значение функции.
- Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
- Функция постоянна, если при всех значениях аргумента значение функции одно и то же.
Промежутки возрастания и убывания функции можно найти по графику.
Вспомним, как выглядит график функции \(\displaystyle y=|x|{\small:}\)
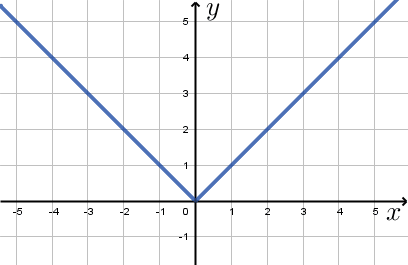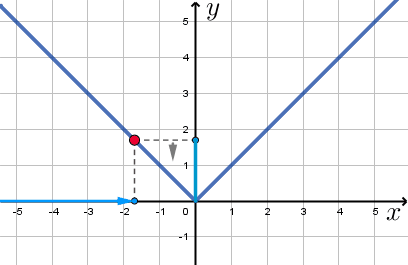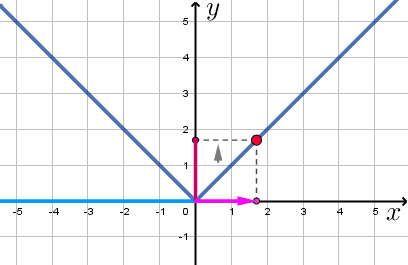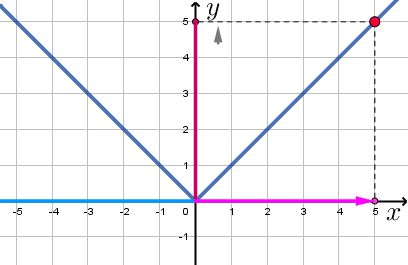
Видим, что
- при увеличении \(\displaystyle x\) от \(\displaystyle -\infty\) до \(\displaystyle 0\) значения \(\displaystyle y\) уменьшаются,
- при увеличении \(\displaystyle x\) от \(\displaystyle 0\) до \(\displaystyle +\infty\) значения \(\displaystyle y\) увеличиваются.
Значит, функция \(\displaystyle y=|x|{\small}\)
- убывает при \(\displaystyle x\in (-\infty; 0]{\small ,}\)
- возрастает при \(\displaystyle x\in [0; +\infty){\small .}\)
| Ответ: | функция убывает на промежутке \(\displaystyle (-\infty; 0]{\small ,}\) |
| функция возрастает на промежутке \(\displaystyle [0; +\infty){\small .}\) |