На рисунке изображен график некоторой прямой пропорциональности:
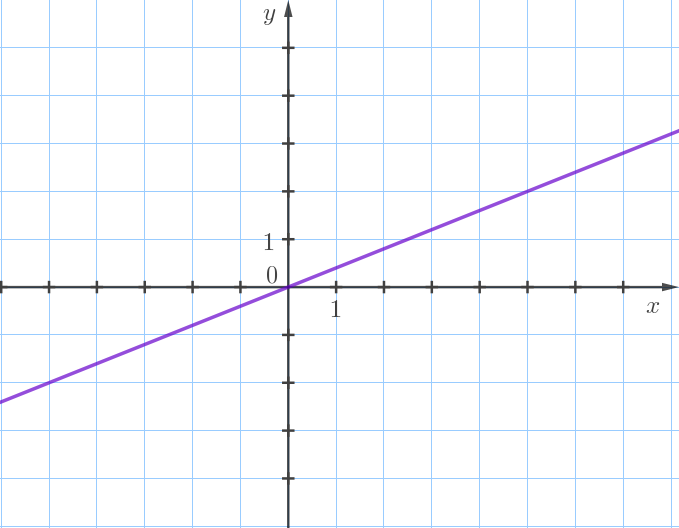
По данному графику напишите соответствующую формулу:
\(\displaystyle y=\)
Прямой пропорциональностью называется функция, которую можно задать формулой
\(\displaystyle y=kx{\small,}\)
где \(\displaystyle x\) – независимая переменная,
\(\displaystyle k\) – не равное нулю число.
На данном графике выберем точку с целочисленными координатами:
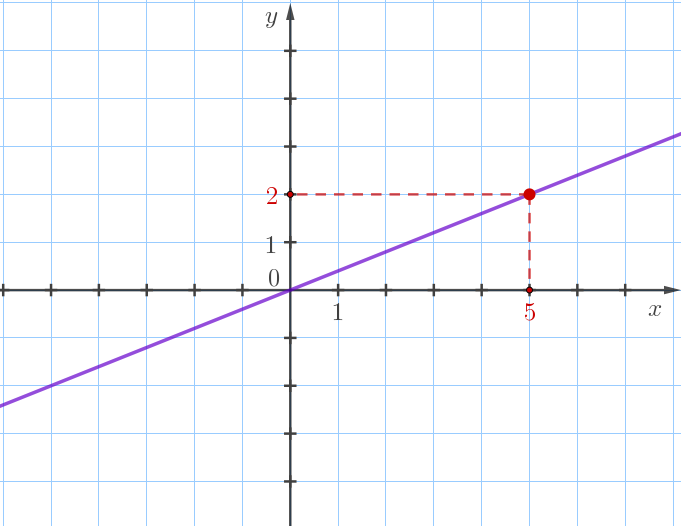
Например, точку с координатами \(\displaystyle (\color{red}{5};\color{red}{2}){\small.}\)
Зададим формулой прямую пропорциональность, график которой проходит через точку \(\displaystyle (\color{red}{5};\color{red}{2}){\small.}\)
Подставим координаты точки \(\displaystyle (\color{red}{5};\color{red}{2})\) в уравнение прямой пропорциональности и определим значение коэффициента \(\displaystyle k{\small:}\)
\(\displaystyle y=kx{\small;}\)
\(\displaystyle \color{red}{2}=k\cdot \color{red}{5}{\small;}\)
\(\displaystyle k=2: 5{\small;}\)
\(\displaystyle k=0{,}4{\small.}\)
Получаем
\(\displaystyle y=0{,}4x{\small.}\)
Ответ: \(\displaystyle y=0{,}4x{\small.}\)