На рисунке изображён график линейной функции \(\displaystyle y=kx+b \small .\)
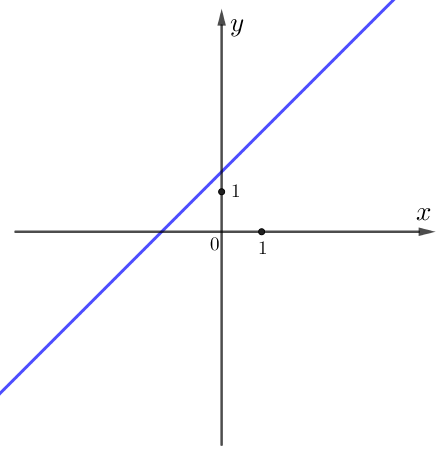
Определите знаки коэффициентов \(\displaystyle k\) и \(\displaystyle b\,{\small : }\)
\(\displaystyle k\) \(\displaystyle 0\)
\(\displaystyle b\) \(\displaystyle 0\)
1. Определим знак коэффициента \(\displaystyle k{\small . }\)
Воспользуемся правилом:
Знак коэффициента \(\displaystyle \small k\) линейной функции \(\displaystyle y= \small {k}x+b\)
- если функция \(\displaystyle y={k}x+ b\) возрастает, то \(\displaystyle {k}>0 \small ;\)
- если функция \(\displaystyle y={k}x+ b\) постоянна, то \(\displaystyle {k}=0 \small ;\)
- если функция \(\displaystyle y={k}x+b\) убывает, то \(\displaystyle {k}<0 \small .\)
По графику видим:
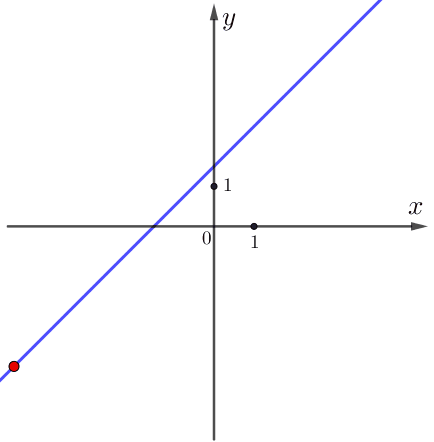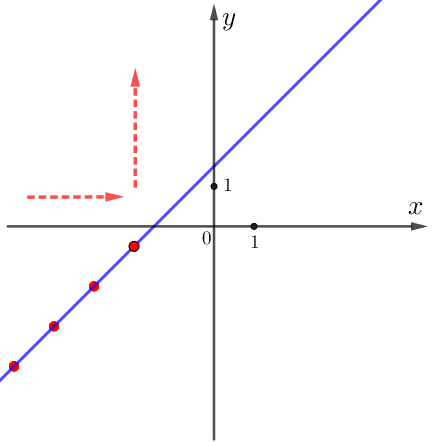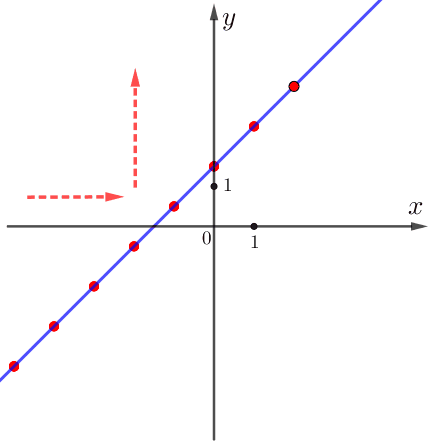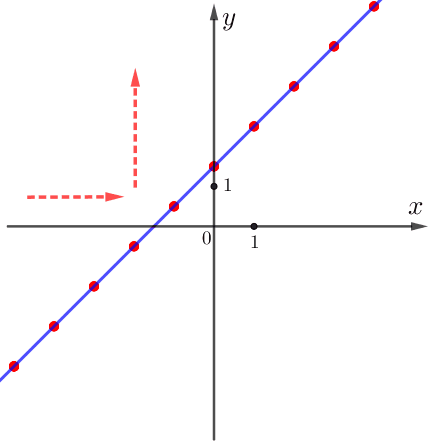
при увеличении значения \(\displaystyle x\) значение \(\displaystyle y=kx+b\) тоже увеличивается.
Значит, функция возрастает и, следовательно:
\(\displaystyle k>0 \small .\)
2. Определим знак коэффициента \(\displaystyle {b \small . }\)
\(\displaystyle b\) – это ордината точки пересечения графика линейной функции \(\displaystyle y=kx+b\) с осью \(\displaystyle Oy{\small .}\)
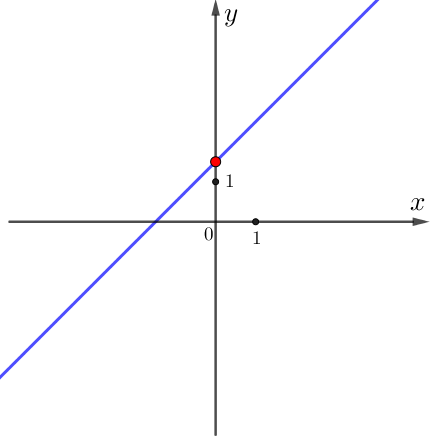
Поскольку точка пересечения находится выше оси \(\displaystyle Ox{\small , }\) её ордината \(\displaystyle {b}\) положительна.
То есть:
\(\displaystyle {b}>0 {\small . }\)
Ответ:\(\displaystyle k>0 \) и \(\displaystyle {b}>0 {\small . }\)