Задание
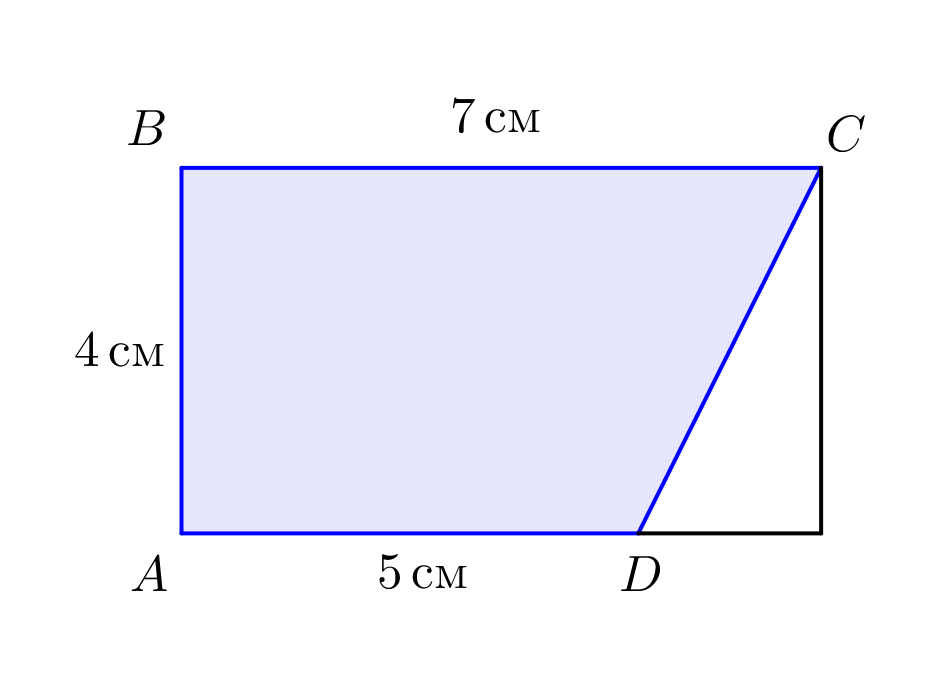
На рисунке изображен четырехугольник \(\displaystyle ABCD\) и даны длины некоторых его сторон. Найдите его площадь.
Ответ запишите в квадратных сантиметрах.
см2.
Решение
Чтобы найти площадь фигуры \(\displaystyle ABCD\small,\) разобьём её на две части: прямоугольник \(\displaystyle ABED\) и треугольник \(\displaystyle ECD\small.\)
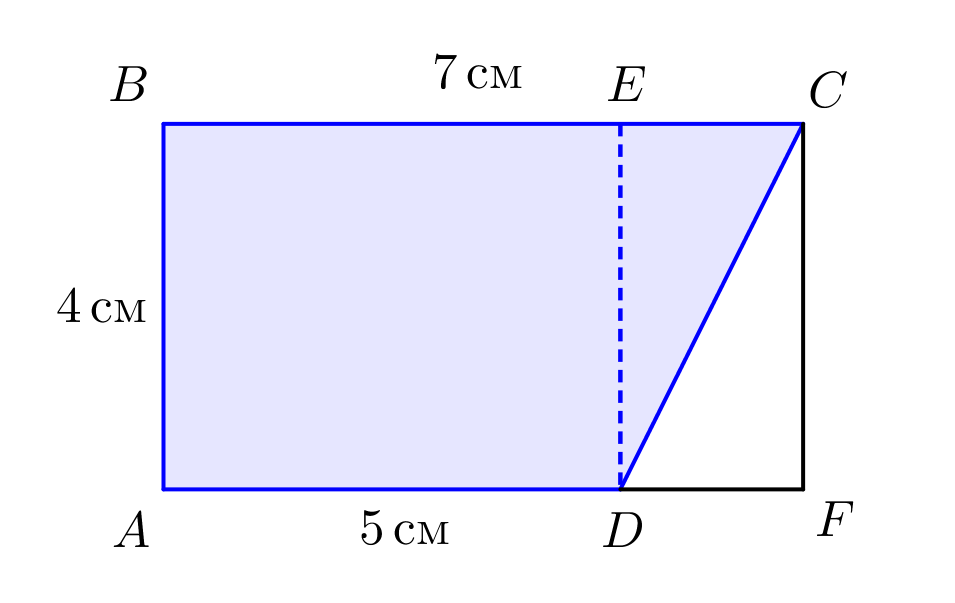
Площадь фигуры \(\displaystyle ABCD\) равна сумме площадей прямоугольника \(\displaystyle ABED\) и треугольника \(\displaystyle ECD\small.\)
Найдем эти площади.
Площадь прямоугольника \(\displaystyle ABED\) равна
\(\displaystyle \color{red}{S_{1}}=5\cdot 4=20\)см2.
Площадь треугольника \(\displaystyle ECD\) равна
\(\displaystyle \color{red}{S_{2}}=(4\cdot 2):2=4\)см2.
Получаем
\(\displaystyle \color{green}S=S_{1}+S_{2}=20+4=24\)см2.
Ответ: \(\displaystyle 24\)см2.