Найдите градусную меру угла между лучом \(\displaystyle OM\) и положительной полуосью \(\displaystyle Ox\small,\) если точка \(\displaystyle M\) имеет координаты \(\displaystyle (-1;\,\sqrt{3}) \small.\)
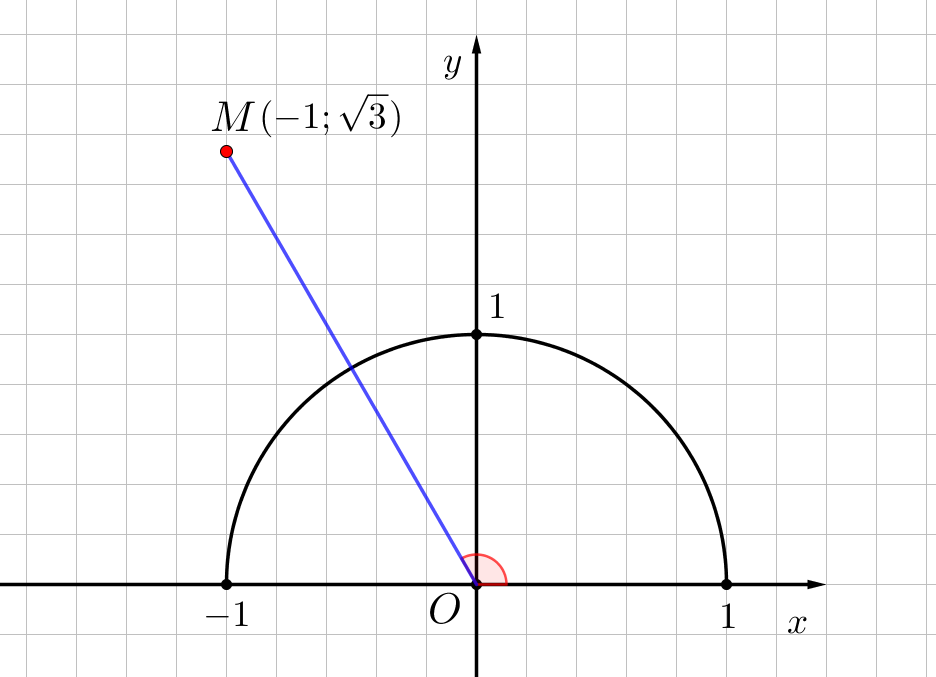
Напомним значения синусов и косинусов некоторых углов:
| \(\displaystyle \alpha\) | \(\displaystyle 30^{\circ}\) | \(\displaystyle 45^{\circ}\) | \(\displaystyle 60^{\circ}\) |
| \(\displaystyle \cos\alpha\) | \(\displaystyle \frac{\sqrt{3}}{2}\) | \(\displaystyle \frac{\sqrt{2}}{2}\) | \(\displaystyle \frac{1}{2}\) |
| \(\displaystyle \sin\alpha\) | \(\displaystyle \frac{1}{2}\) | \(\displaystyle \frac{\sqrt{2}}{2}\) | \(\displaystyle \frac{\sqrt{3}}{2}\) |
\(\displaystyle \angle MOx=\) °
Найдем угол \(\displaystyle MOA\small,\) вычислив его косинус.
Опустим из точки \(\displaystyle M\) высоту на ось абсцисс. Сначала найдем стороны в получившемся прямоугольном треугольнике \(\displaystyle OMA\small.\) Точка \(\displaystyle M\) имеет координаты \(\displaystyle (-1;\,\sqrt{3}) \small,\) тогда катеты равны: \(\displaystyle OA=1\) и \(\displaystyle AM=\sqrt{3}\small.\) | 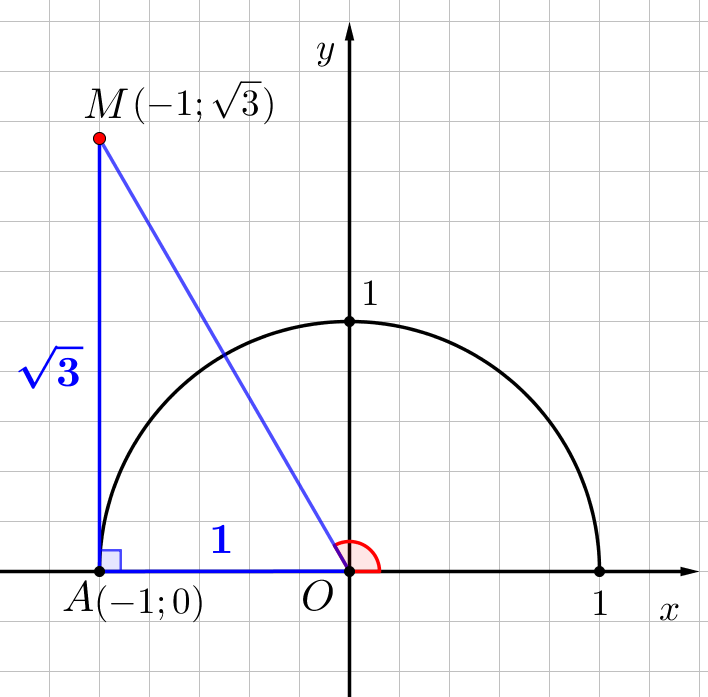 |
\(\displaystyle MO=2\small.\)
Теперь, зная стороны прямоугольного треугольника, найдем косинус угла \(\displaystyle MOA{\small:}\)
\(\displaystyle \cos\angle MOA=\frac{AO}{MO}=\frac{1}{2}\small.\)
Тогда острый угол \(\displaystyle MOA\) равен \(\displaystyle 60^{\circ}{\small:}\)
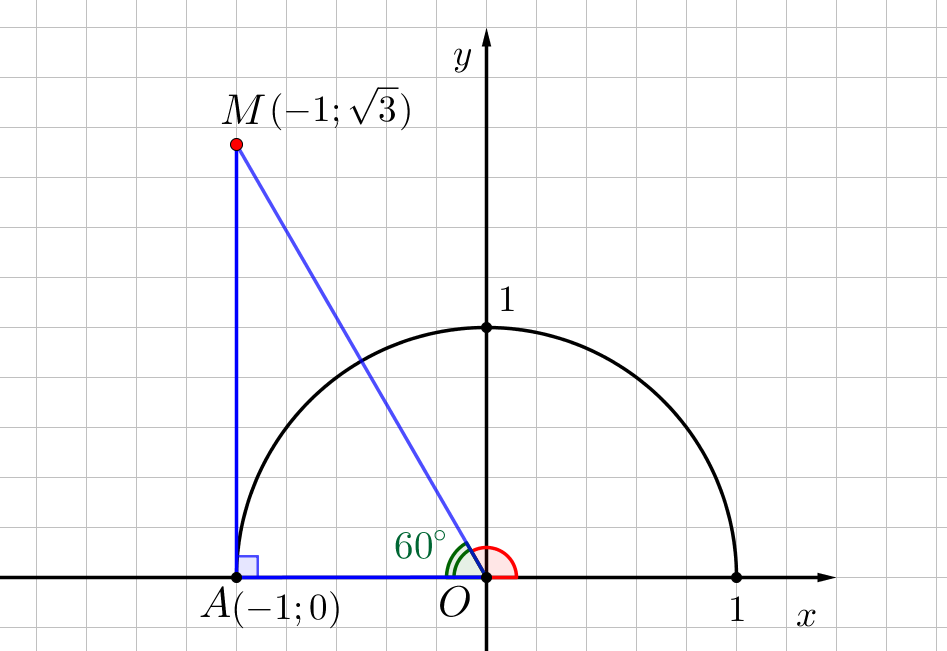
Значит, угол дополняющий \(\displaystyle MOA\) до развернутого, равен
\(\displaystyle \angle MOx=180^{\circ}-\angle MOA=180^{\circ}-60^{\circ}=120^{\circ}\small.\)
Ответ: угол между лучом \(\displaystyle OM\) и положительной полуосью \(\displaystyle Ox\) равен \(\displaystyle 120^{\circ}\small.\)