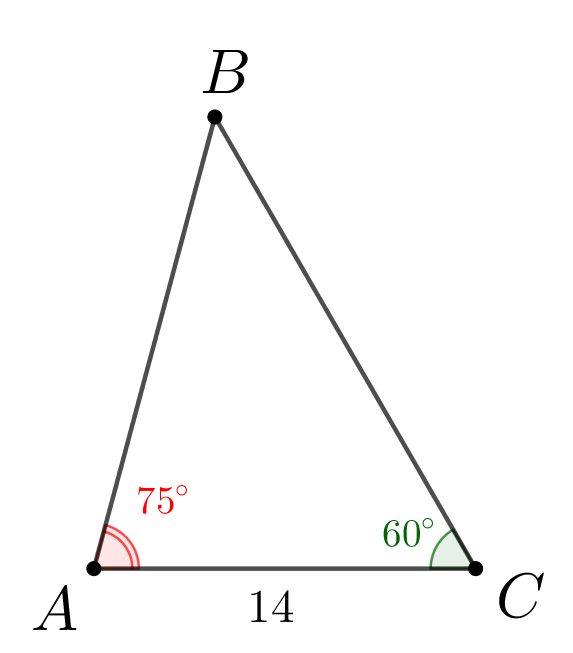
В треугольнике \(\displaystyle ABC\) \(\displaystyle \angle A=75^{\circ}\small,\) \(\displaystyle \angle C=60^{\circ}\small.\) Найдите площадь треугольника \(\displaystyle ABC\small,\) если \(\displaystyle AC=14\small.\)
|  |
Площадь треугольника равна половине произведения стороны (основания) треугольника на высоту, проведенную к этой стороне.
Тогда проведем одну из высот, вычислим ее длину и длину основания.
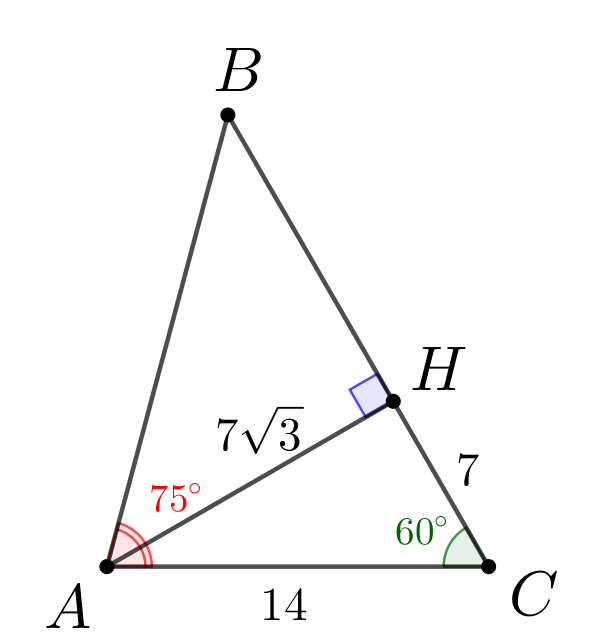
Проведем высоту из вершины \(\displaystyle A\small.\) Получилось два прямоугольных треугольника: \(\displaystyle AHC\) и \(\displaystyle AHB\small.\) В треугольнике \(\displaystyle AHC\) угол \(\displaystyle C\) равен \(\displaystyle 60^{\circ}\) и гипотенуза \(\displaystyle AC=14\small.\) Тогда:
|  |
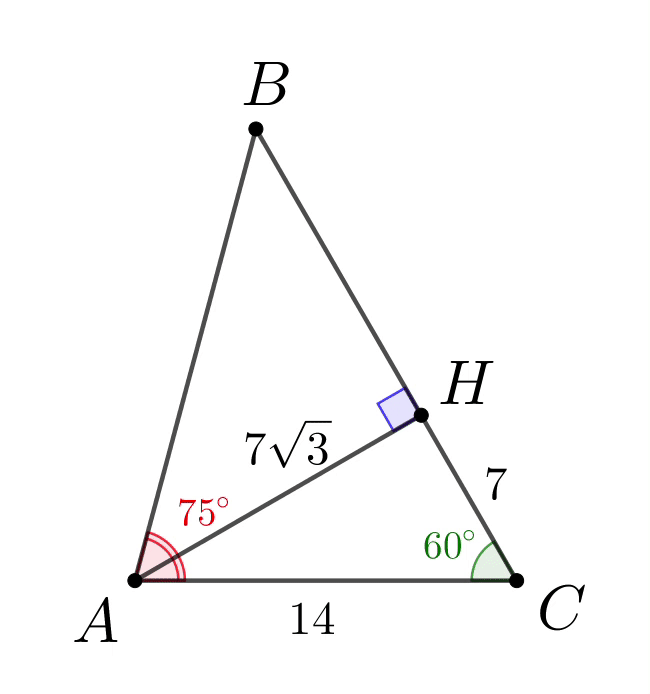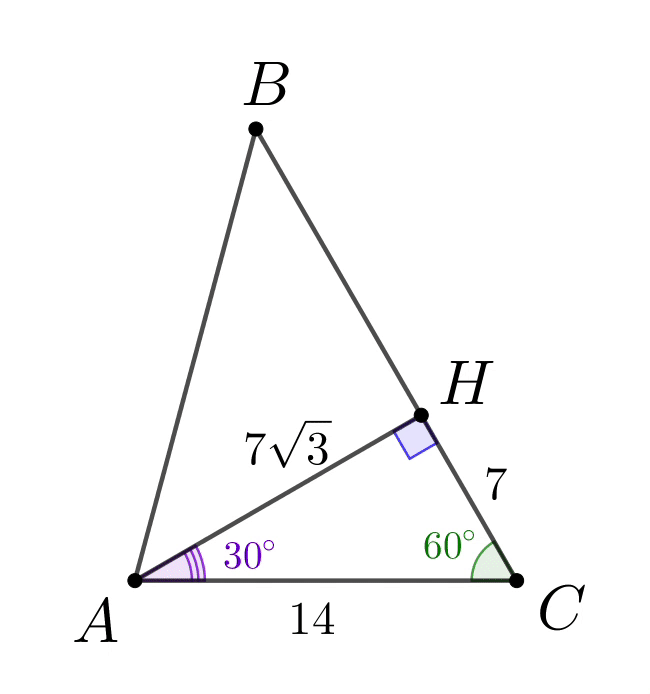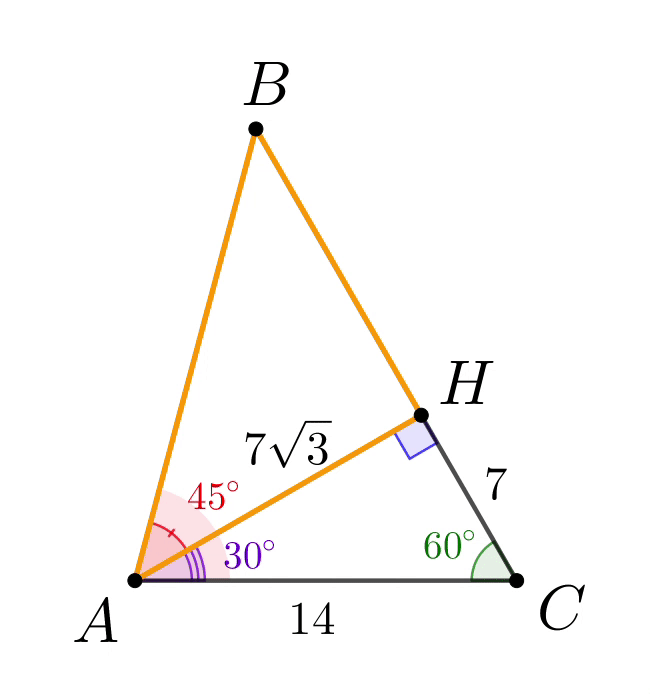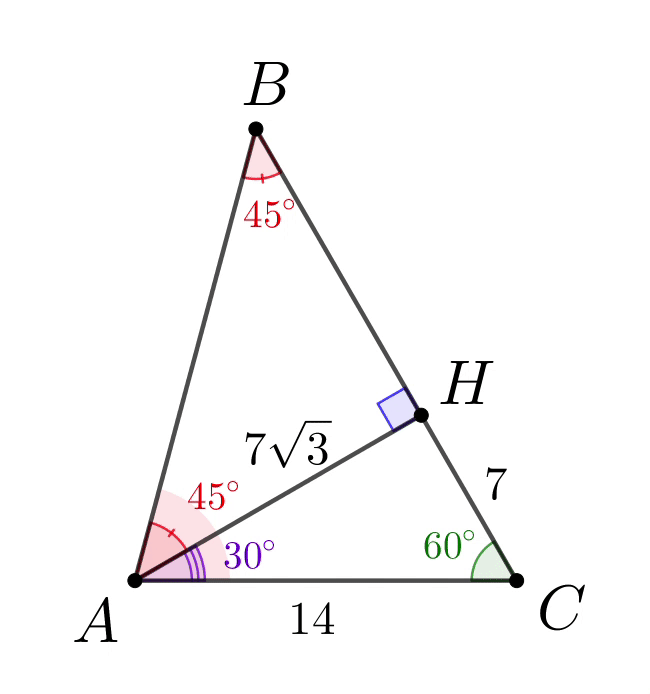
Таким образом, треугольник \(\displaystyle ABH\) равнобедренный: \(\displaystyle \angle BAH=\angle ABH=45^{\circ}\small.\) Тогда \(\displaystyle BH=AH=7\sqrt{3}\small,\) \(\displaystyle BC=BH+HC=7\sqrt{3}+7\small.\) | 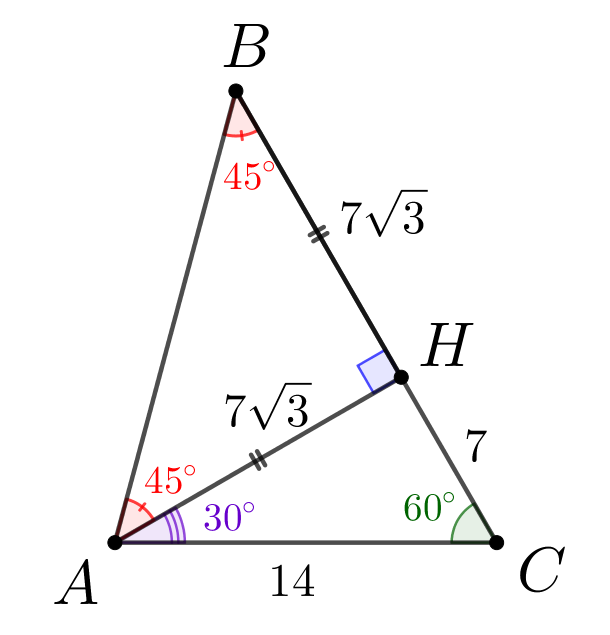 |
Найдем площадь треугольника \(\displaystyle ABC\small{:}\)
\(\displaystyle S_{ABC}=\frac{BC\cdot AH}{2}=\frac{(7\sqrt{3}+7)\cdot7\sqrt{3}}{2}=\frac{49(3+\sqrt{3})}{2}\small.\)
Ответ: \(\displaystyle S_{ABC}=\frac{49(3+\sqrt{3})}{2}\small.\)