В выпуклом четырёхугольнике \(\displaystyle ABCD\) известны длины сторон:
\(\displaystyle AB=10\, {\footnotesize см}{\small,}\) \(\displaystyle BC=12\, {\footnotesize см}{\small,}\) \(\displaystyle CD=14\, {\footnotesize см}{\small,}\) \(\displaystyle AD=16\, {\footnotesize см}{\small.}\)
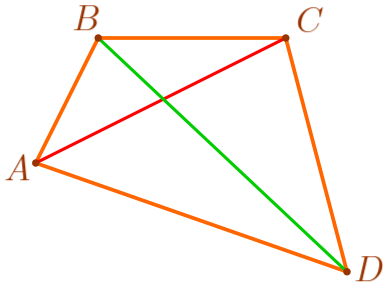
Сформулируйте верное утверждение:
\(\displaystyle AC+BD\) \(\displaystyle 26\, {\footnotesize см}{\small.}\)
Обозначим на рисунке длины сторон четырёхугольника \(\displaystyle ABCD\) и точку \(\displaystyle O\) – точку пересечения диагоналей \(\displaystyle AC\) и \(\displaystyle BD{\small.}\)
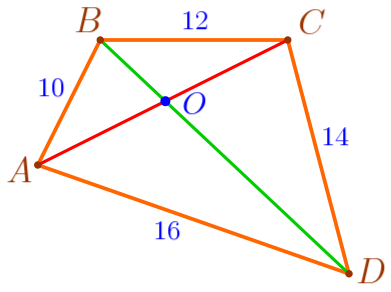
Диагонали разбили четырёхугольник \(\displaystyle ABCD\) на четыре треугольника:
\(\displaystyle \triangle AOB{\small,}\) \(\displaystyle \triangle BOC{\small,}\) \(\displaystyle \triangle COD{\small,}\) \(\displaystyle \triangle AOD{\small.}\)
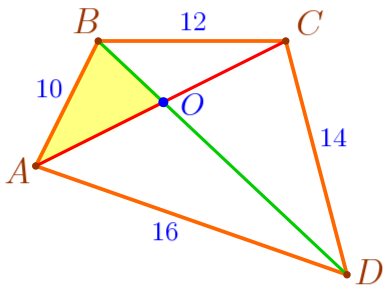 | \(\displaystyle AO+BO>AB{\small;}\) \(\displaystyle AO+BO>10\, {\footnotesize см}{\small.}\) |
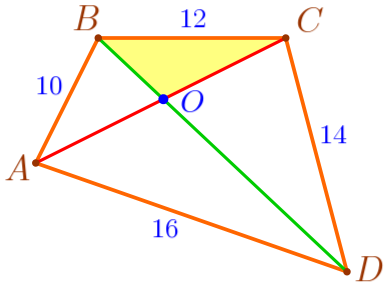 | \(\displaystyle BO+CO>BC{\small;}\) \(\displaystyle BO+CO>12\, {\footnotesize см}{\small.}\) |
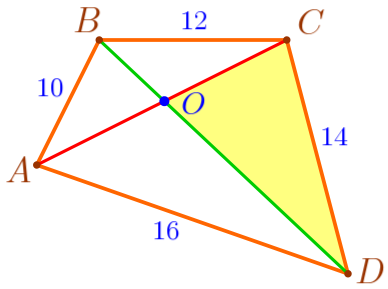 | \(\displaystyle CO+DO>CD{\small;}\) \(\displaystyle CO+DO>14\, {\footnotesize см}{\small.}\) |
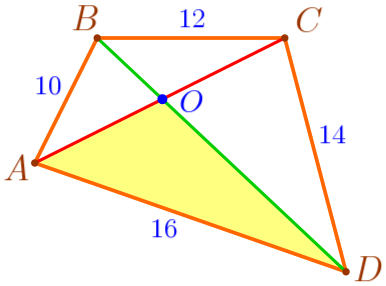 | \(\displaystyle AO+DO>AD{\small;}\) \(\displaystyle AO+DO>16\, {\footnotesize см}{\small.}\) |
Складывая левые и правые части неравенств, получаем:
\(\displaystyle (AO+BO)+(BO+CO)+(CO+DO)+(AO+DO)>10+12+14+16\, {\footnotesize см}{\small;}\)
\(\displaystyle 2 \cdot (AO+BO+CO+DO)>52\, {\footnotesize см}{\small;}\)
\(\displaystyle AO+BO+CO+DO>26\, {\footnotesize см}{\small.}\)
Заметим, что
\(\displaystyle AO+CO=AC\) и \(\displaystyle BO+DO=BD{\small.}\)
То есть
\(\displaystyle AO+BO+CO+DO=AC+BD{\small.}\)
Значит,
\(\displaystyle AC+BD>26\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle AC+BD>26\, {\footnotesize см}{\small.}\)
Сумма длин диагоналей выпуклого четырёхугольника больше половины периметра этого четырёхугольника.