В выпуклом четырёхугольнике \(\displaystyle ABCD\) известны длины сторон:
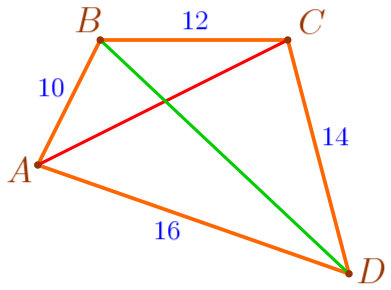
\(\displaystyle AB=10\, {\footnotesize см}{\small,}\) \(\displaystyle BC=12\, {\footnotesize см}{\small,}\) \(\displaystyle CD=14\, {\footnotesize см}{\small,}\) \(\displaystyle AD=16\, {\footnotesize см}{\small.}\)
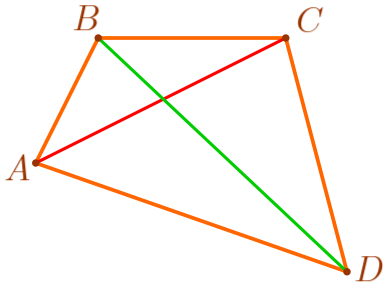
Сформулируйте верное утверждение:
\(\displaystyle AC+BD\) \(\displaystyle 52\, {\footnotesize см}{\small.}\)
Обозначим на рисунке длины сторон четырёхугольника.
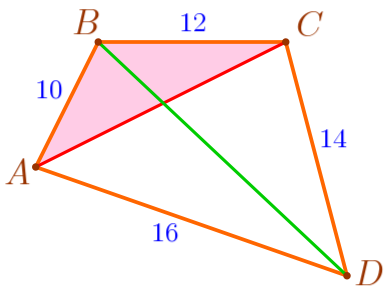 | \(\displaystyle AC<AB+BC{\small;}\) \(\displaystyle AC<10+12{\small;}\) \(\displaystyle AC<22\, {\footnotesize см}{\small.}\) |
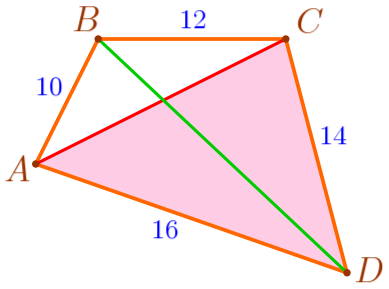 | \(\displaystyle AC<AD+DC{\small;}\) \(\displaystyle AC<16+14{\small;}\) \(\displaystyle AC<30\, {\footnotesize см}{\small.}\) |
Получили
\(\displaystyle AC<22\, {\footnotesize см}{\small}\) и \(\displaystyle AC<30\, {\footnotesize см}{\small.}\)
Значит,
\(\displaystyle AC<22\, {\footnotesize см}{\small.}\)
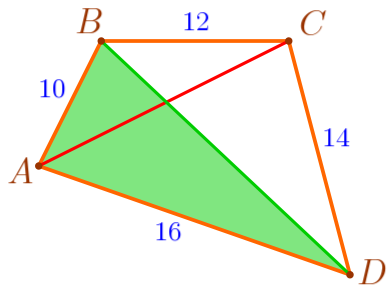 | \(\displaystyle BD<AB+AD{\small;}\) \(\displaystyle BD<10+16{\small;}\) \(\displaystyle BD<26\, {\footnotesize см}{\small.}\) |
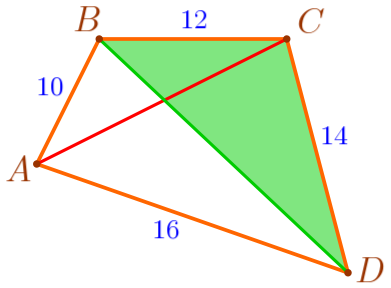 | \(\displaystyle BD<BC+CD{\small;}\) \(\displaystyle BD<12+14{\small;}\) \(\displaystyle BD<26\, {\footnotesize см}{\small.}\) |
Получили
\(\displaystyle BD<26\, {\footnotesize см}{\small.}\)
Оценим сумму длин диагоналей:
\(\displaystyle AC+BD<22+26{\small;}\)
\(\displaystyle AC+BD<48\, {\footnotesize см}{\small.}\)
Так как \(\displaystyle 48\, {\footnotesize см}< 52\, {\footnotesize см}{\small,}\) то
\(\displaystyle AC+BD<52\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle AC+BD<52\, {\footnotesize см}{\small.}\)
Сумма длин диагоналей выпуклого четырёхугольника меньше периметра этого четырёхугольника.