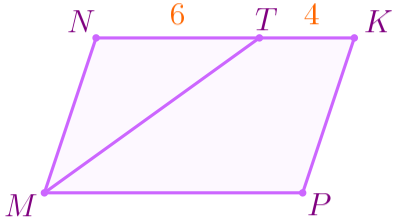
В параллелограмме \(\displaystyle MNKP\) \(\displaystyle MT\) – биссектриса угла \(\displaystyle NMP{\small,}\) \(\displaystyle NT=6\, {\footnotesize см}{\small,} \) \(\displaystyle TK=4\, {\footnotesize см}{\small.} \)
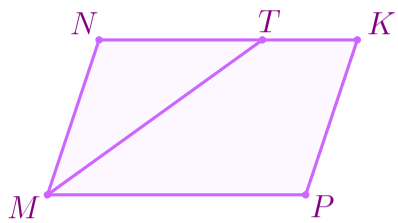
Найдите периметр параллелограмма.
\(\displaystyle {\footnotesize см}{\small.}\)
\(\displaystyle MNKP\) – параллелограмм:
|  |
\(\displaystyle P_{MNKP}=2(MN + NK){\small.}\)
Найдём длины сторон \(\displaystyle MN\) и \(\displaystyle NK{\small:}\)
\(\displaystyle NK=10\, {\footnotesize см}{\small.}\)
\(\displaystyle MN=6\, {\footnotesize см}{\small.}\)
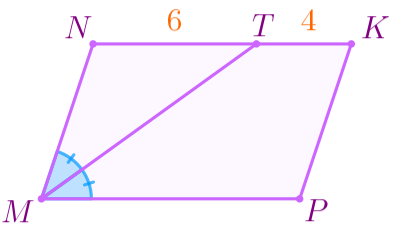
\(\displaystyle \color{blue}{1{\small.}}\) \(\displaystyle MT\) – биссектриса угла \(\displaystyle NMP{\small,}\) значит, \(\displaystyle \angle NMT= \angle PMT{\small.} \) | 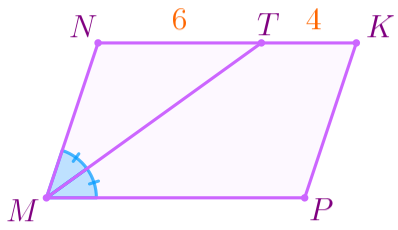 |
\(\displaystyle \color{blue}{2{\small.}}\) По определению, противоположные стороны параллелограмма попарно параллельны: | |
\(\displaystyle MP \parallel NK{\small.}\) Тогда \(\displaystyle \angle PMT=\angle NTM \) как накрест лежащие углы при секущей \(\displaystyle MT{\small.}\) | 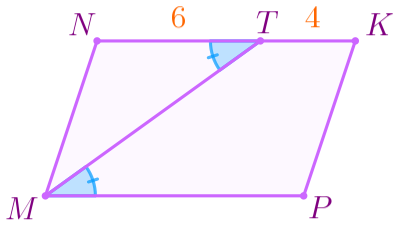 |
| \(\displaystyle \color{blue}{3{\small.}}\) В результате получаем: | |
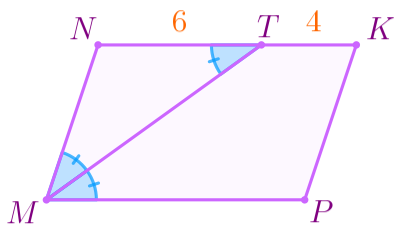 | \(\displaystyle \angle NMT= \angle PMT=\angle NTM{\small.} \) |
| \(\displaystyle \color{blue}{4{\small.}}\) Рассмотрим \(\displaystyle \triangle MNT{\small:}\) | |
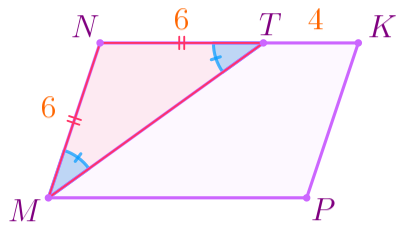 | Так как \(\displaystyle \angle NMT=\angle NTM{\small,} \) то \(\displaystyle \triangle MNT\) – равнобедренный. |
\(\displaystyle MN=NT=6\, {\footnotesize см}{\small.} \)
Подставим в формулу периметра \(\displaystyle MN=6\, {\footnotesize см}{\small,} \) \(\displaystyle NK=10\, {\footnotesize см}{\small:}\)
\(\displaystyle P_{MNKP}=2(MN + NK){\small,}\)
\(\displaystyle P_{MNKP}=2 \cdot (6+ 10)=2 \cdot 16=32\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle 32\, {\footnotesize см}{\small.}\)