Теория: Биссектрисы углов (короткая версия)

По условию задачи выполним построение:

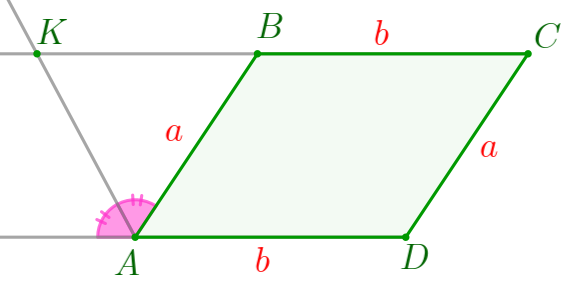\(\displaystyle ABCD\) – параллелограмм: \(\displaystyle AB=DC=a{\small;}\) \(\displaystyle AD=BC=b{\small;}\) \(\displaystyle AK\) – биссектриса внешнего угла при вершине \(\displaystyle A{\small;}\) \(\displaystyle K\) – точка пересечения биссектрисы \(\displaystyle AK\) и продолжения стороны \(\displaystyle BC{\small.}\)

Периметр параллелограмма \(\displaystyle ABCD\) равен \(\displaystyle 34\, {\footnotesize см}{\small.}\) То есть

\(\displaystyle 2(a+b)=34\, {\footnotesize см}{\small.}\)

Требуется найти длину отрезка \(\displaystyle CK{\small.}\)

Так как точка \(\displaystyle K\) лежит на продолжении стороны \(\displaystyle BC{\small,}\) то

\(\displaystyle CK=BC+BK{\small.}\)

На продолжении стороны \(\displaystyle AD\) за точку \(\displaystyle A\) отметим точку \(\displaystyle E{\small.}\)

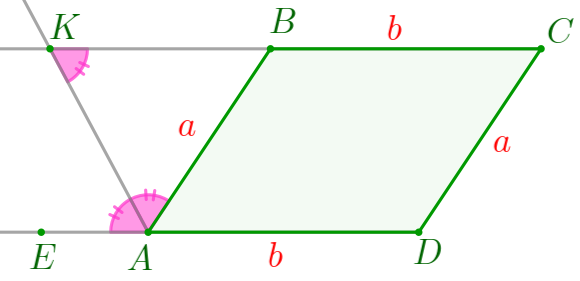\(\displaystyle \angle BAK= \angle EAK{\small,} \) так как \(\displaystyle AK\) – биссектриса угла \(\displaystyle BAE{\small;}\) \(\displaystyle \angle EAK=\angle BKA \) как накрест лежащие углы при параллельных прямых \(\displaystyle AD\) и \(\displaystyle BC\) и секущей \(\displaystyle AK{\small.}\)

Следовательно,

\(\displaystyle \angle BAK= \angle EAK=\angle BKA{\small.} \)

 

Рассмотрим треугольник \(\displaystyle ABK{\small:}\)

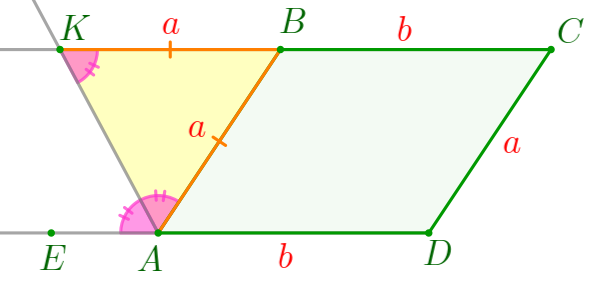Так как  \(\displaystyle \angle BAK= \angle BKA{\small,} \) то \(\displaystyle \triangle ABK\) – равнобедренный. Значит, \(\displaystyle BK=AB=a{\small.}\)

В результате получаем:

\(\displaystyle CK=BC+BK=b+a{\small.}\)

По условию

\(\displaystyle 2(a+b)=34\, {\footnotesize см}{\small,}\)

значит,

\(\displaystyle a+b=17\, {\footnotesize см}{\small.}\)

То есть

\(\displaystyle CK=17\, {\footnotesize см}{\small.}\)

Ответ: \(\displaystyle 17\, {\footnotesize см}{\small.}\)