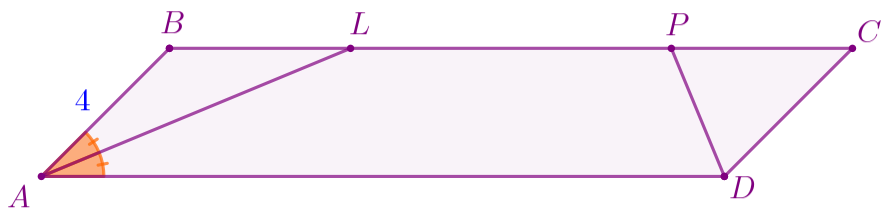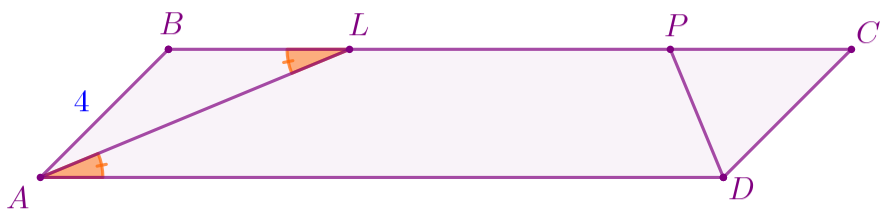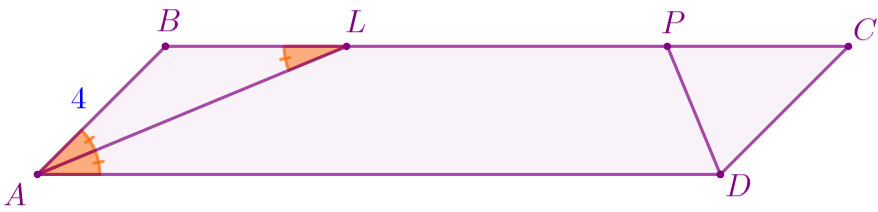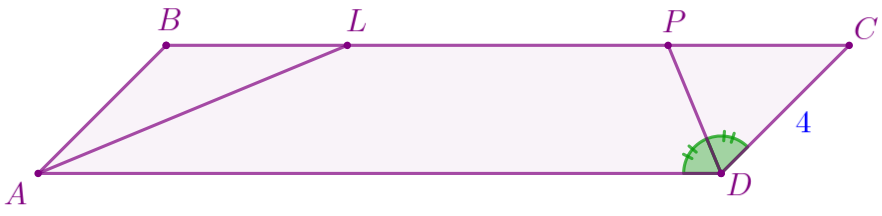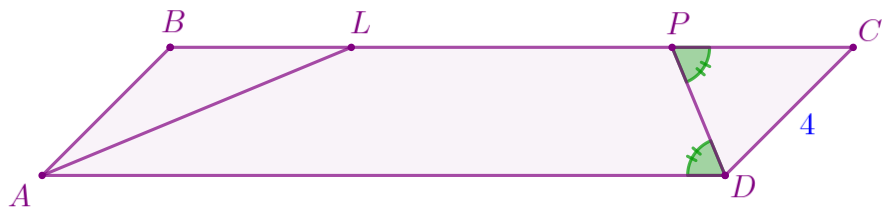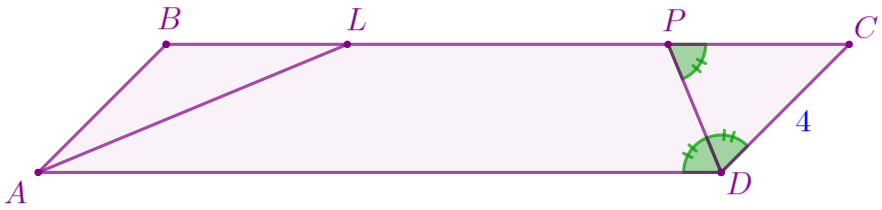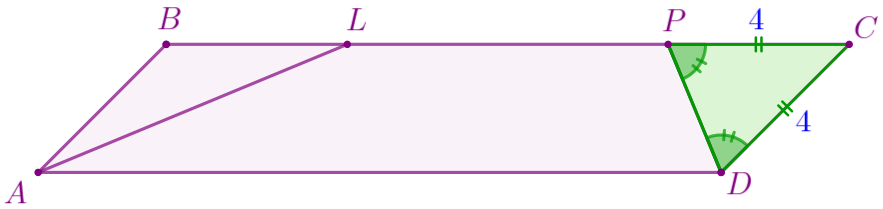Стороны параллелограмма равны \(\displaystyle 15\, \footnotesize см\) и \(\displaystyle 4\, \footnotesize см{\small.}\) Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.
\(\displaystyle ;\) \(\displaystyle ;\) \(\displaystyle .\)
По условию задачи выполним построение.
Пусть \(\displaystyle ABCD\) – параллелограмм, в котором:
- \(\displaystyle AD=BC=15\, {\footnotesize см}{\small;}\)
- \(\displaystyle AB=CD=4\, {\footnotesize см}{\small;}\)
- \(\displaystyle AL\) – биссектриса угла \(\displaystyle BAD{\small;}\)
- \(\displaystyle DP\) – биссектриса угла \(\displaystyle ADC{\small.}\)
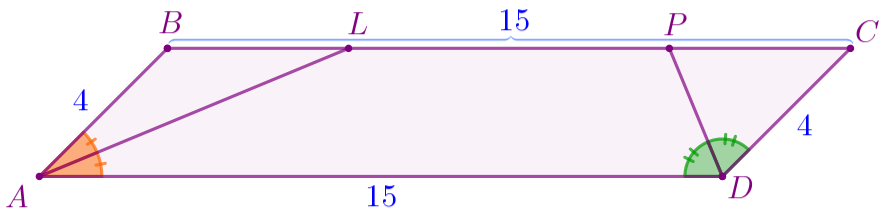
Требуется найти длины отрезков \(\displaystyle BL{\small,}\) \(\displaystyle LP\) и \(\displaystyle PC{\small.}\)
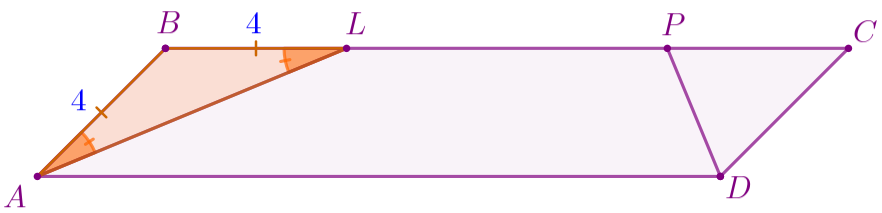
\(\displaystyle BL=4\, {\footnotesize см}{\small.}\)
\(\displaystyle PC=4\, {\footnotesize см}{\small.}\)
\(\displaystyle LP=7\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle 4\, {\footnotesize см}{\small;} \) \(\displaystyle 7\, {\footnotesize см}{\small;} \) \(\displaystyle 4\, {\footnotesize см}{\small.} \)