Решите треугольник \(\displaystyle ABC\small,\) в котором \(\displaystyle \angle A=80^{\circ},\, \angle B=70^{\circ}\) и \(\displaystyle AB=18\small.\)
(То есть найдите все остальные элементы треугольника.)
Сразу отметим, что поскольку сумма углов в треугольнике \(\displaystyle 180^{\circ}\small,\) то третий неизвестный угол равен: \(\displaystyle \angle C=180^{\circ}-80^{\circ}-70^{\circ}=30^{\circ}\small.\) | 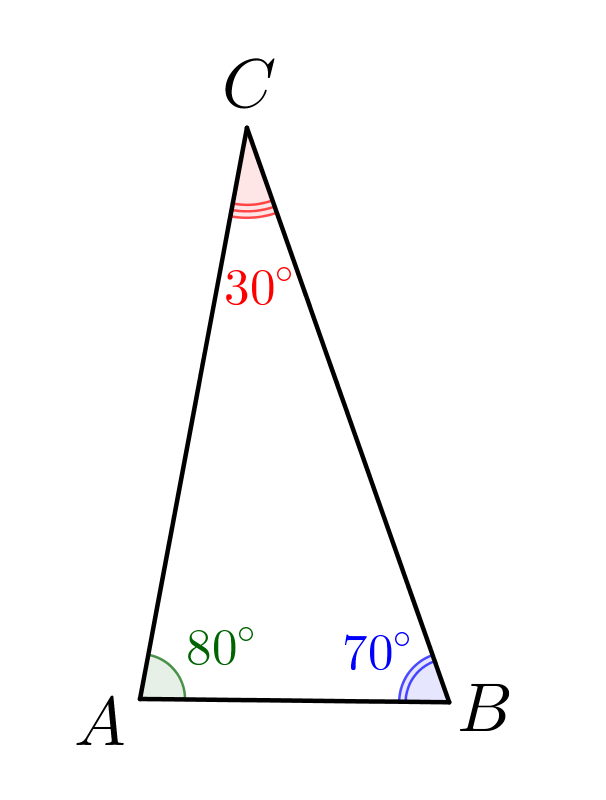 |
Чтобы найти стороны треугольника, воспользуемся теоремой синусов:
Теорема синусов
В треугольнике отношения сторон к синусам противолежащих углов одинаковы и равны удвоенному радиусу описанной окружности: \(\displaystyle \frac{\color{Purple}{a}}{\sin\color{Purple}{\alpha}}=\frac{\color{green}{b}}{\sin\color{green}{\beta}}=\frac{\color{blue}{c}}{\sin\color{blue}{\gamma}}=2\color{red}{R}{\small.}\) | 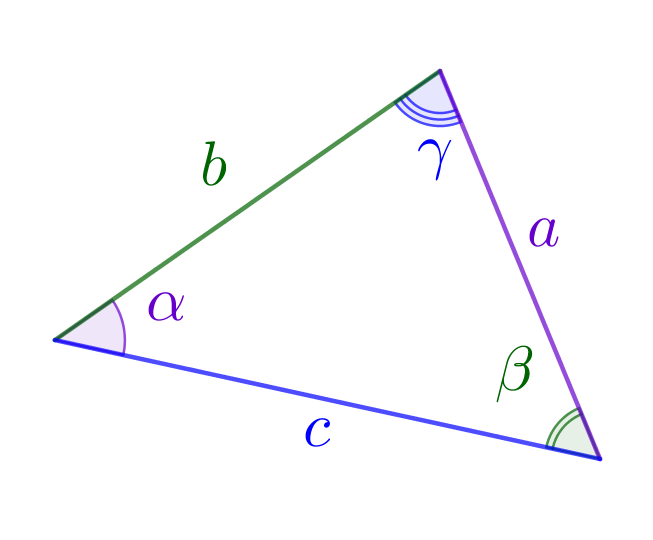 |
Подставляя значения, получаем:
\(\displaystyle \frac{BC}{\sin80^{\circ}}=\frac{AC}{\sin70^{\circ}}=\frac{18}{\sin30^{\circ}}\small.\)
Поскольку, \(\displaystyle \sin30^{\circ}=\frac{1}{2}\small,\) то
\(\displaystyle \frac{18}{\sin30^{\circ}}=18:\frac{1}{2}=36\small.\)
Тогда
- \(\displaystyle \frac{BC}{\sin80^{\circ}}=36\) и \(\displaystyle BC=36\sin80^{\circ}\small,\)
- \(\displaystyle \frac{AC}{\sin70^{\circ}}=36\) и \(\displaystyle AC=36\sin70^{\circ}\small.\)