Периметр равнобедренного треугольника с углом \(\displaystyle 120^{\circ}\) равен \(\displaystyle 26\small.\) Найдите стороны этого треугольника.
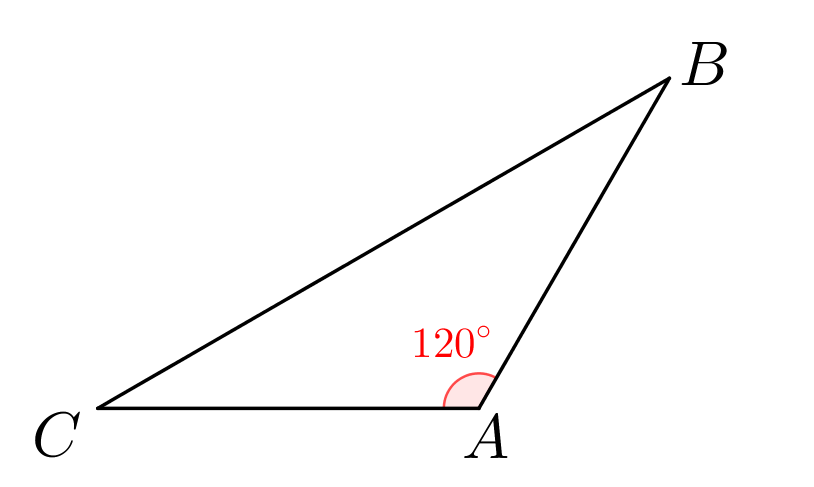
Треугольник \(\displaystyle ABC\) – равнобедренный. Значит, два его угла равны. Угол \(\displaystyle A\) тупой, а двух тупых углов в треугольнике быть не может. Тогда \(\displaystyle \angle B=\angle C=\frac{180^{\circ}-\angle A}{2}=30^{\circ}\small.\)
Обозначим одну из сторон за \(\displaystyle x\) и выразим через \(\displaystyle x\) остальные стороны, используя теорему синусов. |  |
Получаем:
\(\displaystyle \frac{x}{\sin120^{\circ}}=\frac{AB}{\sin30^{\circ}}=\frac{AC}{\sin30^{\circ}}\small.\)
Получаем:
\(\displaystyle AB=AC=\frac{x}{\sin120^{\circ}}\cdot \sin30^{\circ}=\frac{x}{\sqrt{3}}\small.\)
Поскольку периметр треугольника равен сумме длин сторон, то
\(\displaystyle P_{ABC}=AB+BC+AC\small.\)
Подставляя известные значения, получаем:
\(\displaystyle 26=\frac{x}{\sqrt{3}}+x+\frac{x}{\sqrt{3}}=x\left(1+\frac{2}{\sqrt{3}}\right)\small,\)
\(\displaystyle x=\frac{26}{\left(1+\frac{2}{\sqrt{3}}\right)}=\frac{26\sqrt{3}}{\sqrt{3}+2}\small.\)
\(\displaystyle x=52\sqrt3-78\small.\)
Тогда
\(\displaystyle BC=52\sqrt3-78\) и \(\displaystyle AB=AC=\frac{52\sqrt3-78}{\sqrt{3}}=52-26\sqrt{3}\small.\)