Задание
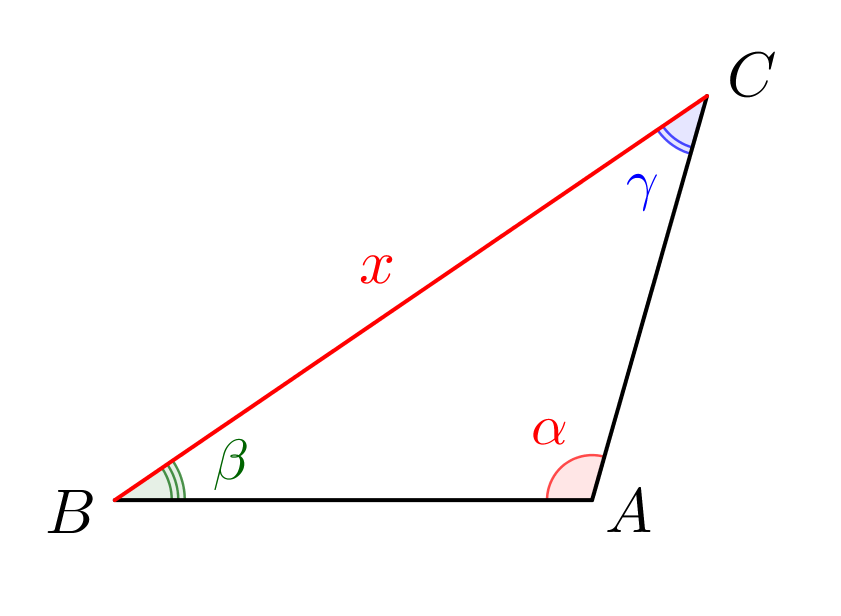
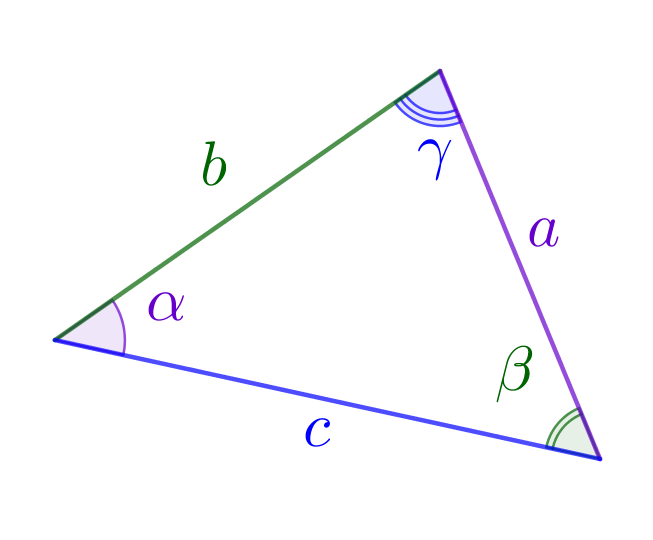
Углы треугольника равны \(\displaystyle \alpha,\,\beta,\,\gamma\small,\) а периметр равен \(\displaystyle P\small.\) Найдите стороны этого треугольника.
\(\displaystyle AB=\)
, \(\displaystyle AC=\)
и \(\displaystyle BC=\)
Решение
Обозначим одну из сторон за \(\displaystyle x\) и выразим через \(\displaystyle x\) остальные стороны, используя теорему синусов.
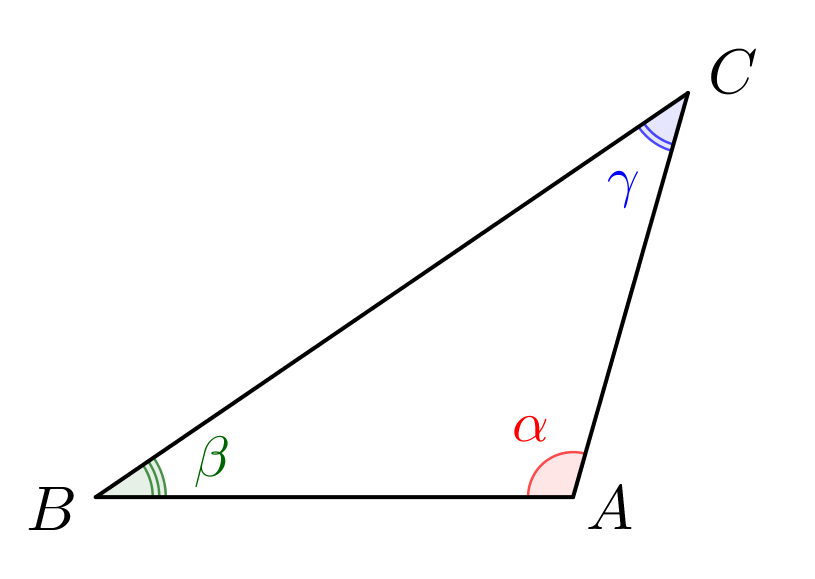
Получаем:
\(\displaystyle \frac{x}{\sin\alpha}=\frac{AC}{\sin\beta}=\frac{AB}{\sin\gamma}\small.\)
Выразим \(\displaystyle AB\) и \(\displaystyle AC\) через \(\displaystyle x{\small:}\)
- \(\displaystyle AC=\frac{x}{\sin\alpha}\cdot\sin\beta=\frac{x\sin\beta}{\sin\alpha}\small,\)
- \(\displaystyle AB=\frac{x}{\sin\alpha}\cdot\sin\gamma=\frac{x\sin\gamma}{\sin\alpha}\small.\)
Поскольку периметр треугольника равен сумме длин сторон, то
\(\displaystyle P_{ABC}=AB+BC+AC\small.\)
Подставляя известные значения, получаем:
\(\displaystyle P=x+\frac{x\sin\beta}{\sin\alpha}+\frac{x\sin\gamma}{\sin\alpha}=x\left(\frac{\sin\alpha+\sin\beta+\sin\gamma}{\sin\alpha}\right)\small,\)
\(\displaystyle x=\frac{P\sin\alpha}{\sin\alpha+\sin\beta+\sin\gamma}\small.\)
Тогда
- \(\displaystyle BC=\frac{P\sin\alpha}{\sin\alpha+\sin\beta+\sin\gamma}\small,\)
- \(\displaystyle AC=\frac{\frac{P\sin\alpha}{\sin\alpha+\sin\beta+\sin\gamma}\cdot\sin\beta}{\sin\alpha}=\frac{P\sin\beta}{\sin\alpha+\sin\beta+\sin\gamma}\small,\)
- \(\displaystyle AB=\frac{\frac{P\sin\alpha}{\sin\alpha+\sin\beta+\sin\gamma}\cdot\sin\gamma}{\sin\alpha}=\frac{P\sin\gamma}{\sin\alpha+\sin\beta+\sin\gamma}\small.\)