На сторонах \(\displaystyle KL\) и \(\displaystyle NM\) параллелограмма \(\displaystyle KLMN\) отмечены соответственно точки \(\displaystyle Q\) и \(\displaystyle P\) так, что \(\displaystyle \angle NQL= \angle LPN{\small.}\)
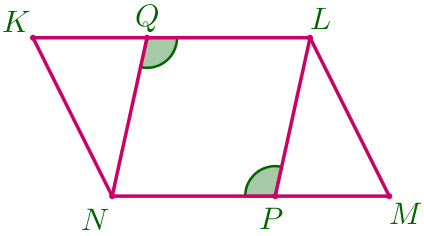
\(\displaystyle \color{red}{1.}\) Является ли четырёхугольник \(\displaystyle NQLP\) параллелограммом?
Почему?
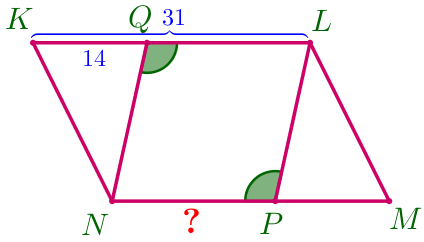
\(\displaystyle \color{red}{2.}\) Найдите длину отрезка \(\displaystyle NP{\small,}\) если \(\displaystyle KL=31{\small,}\) \(\displaystyle KQ=14{\small.}\)
\(\displaystyle NP=\)
|  |
\(\displaystyle \color{red}{1.}\) Определим, является ли четырёхугольник \(\displaystyle NQLP\) параллелограммом.
Если у четырёхугольника противоположные углы попарно равны, то он является параллелограммом. | 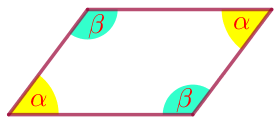 |
По условию в четырёхугольнике \(\displaystyle NQLP\) два противоположных угла \(\displaystyle \color{green}{ NQL}\) и \(\displaystyle \color{green}{ LPN}\) равны.
Выясним, равны ли два других угла.
\(\displaystyle KL \parallel MN{\small.}\)
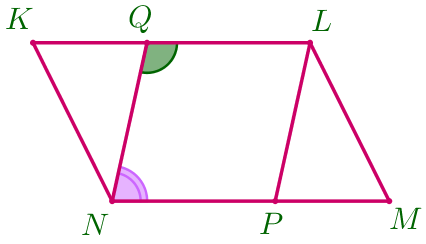 | \(\displaystyle \color{darkviolet}{\angle QNP}\) и \(\displaystyle \color{green}{\angle NQL}\) – односторонние углы при секущей \(\displaystyle QN{\small.}\) Значит, \(\displaystyle \color{darkviolet}{\angle QNP}=180^{\circ} -\color{green}{\angle NQL}{\small.}\) |
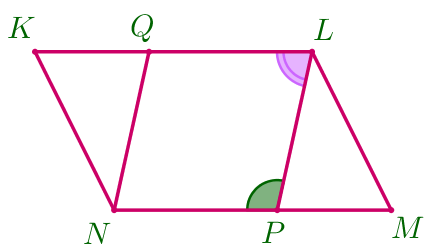 | \(\displaystyle \color{darkviolet}{\angle QLP}\) и \(\displaystyle \color{green}{\angle LPN}\) – односторонние углы при секущей \(\displaystyle LP{\small.}\) Значит, \(\displaystyle \color{darkviolet}{\angle QLP}=180^{\circ}-\color{green}{\angle LPN} {\small.}\) |
\(\displaystyle \color{darkviolet}{\angle QNP}=\color{darkviolet}{ \angle QLP}{\small.}\)
В результате получаем
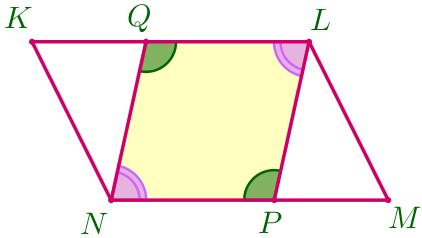 | \(\displaystyle \color{green}{\angle NQL}=\color{green}{ \angle LPN}{\small,}\) \(\displaystyle \color{darkviolet}{\angle QNP}=\color{darkviolet}{ \angle QLP}{\small.}\) |
В четырёхугольнике \(\displaystyle NQLP\) противоположные углы попарно равны.
Следовательно,
\(\displaystyle NQLP\) – параллелограмм.
\(\displaystyle \color{red}{2.}\) Найдём длину отрезка \(\displaystyle NP{\small.}\)
Так как \(\displaystyle NP\) и \(\displaystyle QL\) – противоположные стороны параллелограмма \(\displaystyle NQLP{\small,}\) то
\(\displaystyle NP=QL{\small.}\)
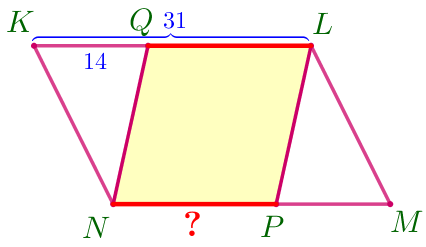 | Точка \(\displaystyle Q\) лежит на стороне \(\displaystyle KL{\small,}\) тогда \(\displaystyle QL=KL-KQ{\small.}\) Подставим \(\displaystyle KL=31{\small,}\) \(\displaystyle KQ=14{\small:}\) \(\displaystyle QL=31-14=17{\small.}\) |
Значит,
\(\displaystyle NP=17{\small.}\)
| Ответ: | \(\displaystyle \color{red}{1.}\) | Является ли четырёхугольник \(\displaystyle NQLP\) параллелограммом? Да. Почему? Противоположные углы попарно равны. |
| \(\displaystyle \color{red}{2.}\) | \(\displaystyle NP=17{\small.}\) |