На сторонах \(\displaystyle MB\) и \(\displaystyle KD\) параллелограмма \(\displaystyle MBKD\) отмечены соответственно точки \(\displaystyle A\) и \(\displaystyle C\) так, что \(\displaystyle \angle ADM= \angle CBK{\small.}\)
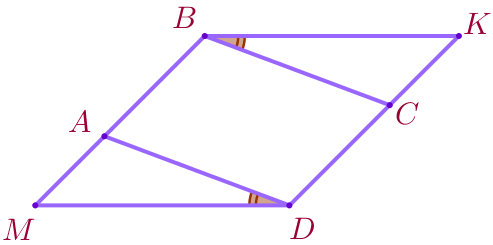
\(\displaystyle \color{red}{1.}\) Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом?
Почему?
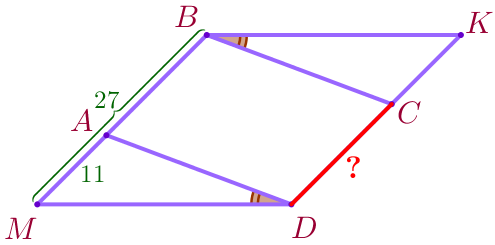
\(\displaystyle \color{red}{2.}\) Найдите длину отрезка \(\displaystyle CD{\small,}\) если \(\displaystyle MB=27{\small,}\) \(\displaystyle AM=11{\small.}\)
\(\displaystyle CD=\)
|  |
Так как \(\displaystyle MBKD\) – параллелограмм по условию, то
\(\displaystyle MB\parallel KD{\small,}\) \(\displaystyle BK\parallel MD{\small;}\)
\(\displaystyle \angle MBK=\angle MDK{\small,}\) \(\displaystyle \angle BMD=\angle BKD{\small.}\)
\(\displaystyle \color{red}{1.}\) Определим, является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом.
Если у четырёхугольника противоположные углы попарно равны, то он является параллелограммом. |  |
Проверим, равны ли противоположные углы четырёхугольника \(\displaystyle ABCD?\)
Рассмотрим углы \(\displaystyle ABC\) и \(\displaystyle ADC{\small.}\)
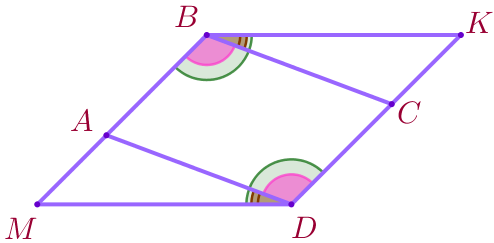 |
|
\(\displaystyle \color{magenta}{\angle ABC}=\color{magenta}{\angle ADC}{\small.}\)
Рассмотрим углы \(\displaystyle BAD\) и \(\displaystyle BCD{\small.}\)
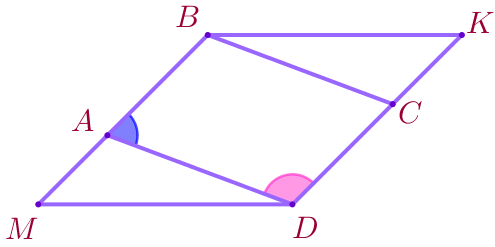 | Углы \(\displaystyle BAD\) и \(\displaystyle ADC\) – односторонние при секущей \(\displaystyle AD{\small.}\) Значит, \(\displaystyle \angle BAD=180^{\circ}-\color{magenta}{\angle ADC}{\small.}\) |
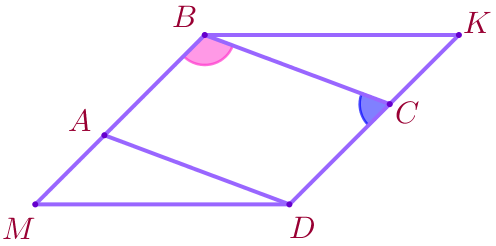 | Углы \(\displaystyle BCD\) и \(\displaystyle ABC\) – односторонние при секущей \(\displaystyle BC{\small.}\) Значит, \(\displaystyle \angle BCD=180^{\circ}-\color{magenta}{\angle ABC}{\small.}\) |
\(\displaystyle \color{blue}{\angle BAD}=\color{blue}{\angle BCD}{\small.}\)
В результате получаем
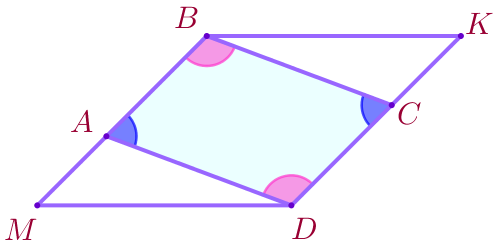 | \(\displaystyle \color{magenta}{\angle ABC}=\color{magenta}{\angle ADC }{\small,}\) \(\displaystyle \color{blue}{\angle BAD}=\color{blue}{\angle BCD}{\small.}\) |
В четырёхугольнике \(\displaystyle ABCD\) противоположные углы попарно равны.
Следовательно,
\(\displaystyle ABCD\) – параллелограмм.
\(\displaystyle \color{red}{2.}\) Найдём длину отрезка \(\displaystyle CD{\small.}\)
Так как \(\displaystyle CD\) и \(\displaystyle AB\) – противоположные стороны параллелограмма \(\displaystyle ABCD{\small,}\) то
\(\displaystyle CD=AB{\small.}\)
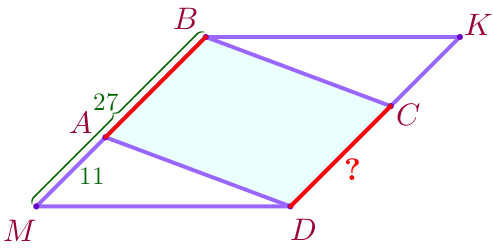 | Точка \(\displaystyle A\) лежит на стороне \(\displaystyle MB{\small,}\) тогда \(\displaystyle AB=MB-AM{\small.}\) Подставим \(\displaystyle MB=27{\small,}\) \(\displaystyle AM=11{\small:}\) \(\displaystyle AB=27-11=16{\small.}\) |
Значит,
\(\displaystyle CD=16{\small.}\)
| Ответ: | \(\displaystyle \color{red}{1.}\) | Является ли четырёхугольник \(\displaystyle ABCD\) параллелограммом? Да. Почему? Противоположные углы попарно равны. |
| \(\displaystyle \color{red}{2.}\) | \(\displaystyle CD=16{\small.}\) |