Две медианы треугольника равны \(\displaystyle 6\) и \(\displaystyle 9\) и пересекаются под углом \(\displaystyle 120^{\circ}\small.\) Найдите стороны этого треугольника.
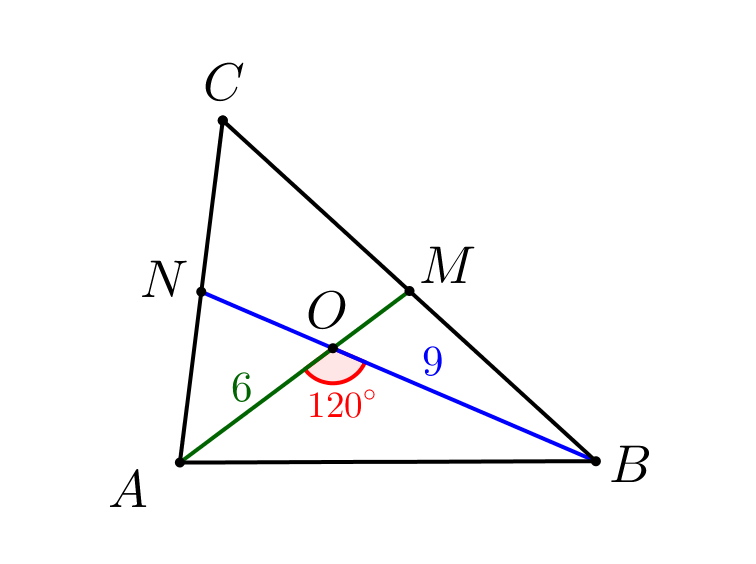
- \(\displaystyle AB=\)
- \(\displaystyle AC=\)
- \(\displaystyle BC=\)
Сразу отметим, что медианы точкой пересечения делятся в отношении \(\displaystyle 2:1\small.\) Тогда:
| 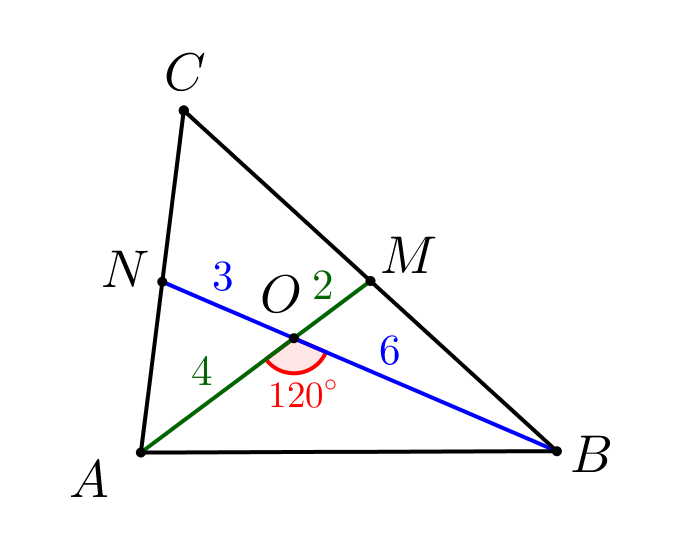 |
\(\displaystyle AB=2\sqrt{19}\small.\)
Запишем теорему косинусов для треугольника \(\displaystyle AOB\) и стороны \(\displaystyle AB{\small:}\)
\(\displaystyle AB^2=AO^2+BO^2-2\cdot AO\cdot BO\cdot\cos120^{\circ}\small.\)
Подставим известные значения. Поскольку \(\displaystyle \cos120^{\circ}=-\cos(180^{\circ}-120^{\circ})=-\cos60^{\circ}=-\frac{1}{2}\small,\) получаем:
\(\displaystyle AB^2=4^2+6^2-2\cdot4\cdot6\cdot\left(-\frac{1}{2}\right)=76\small,\)
\(\displaystyle AB=\sqrt{76}=2\sqrt{19}\small.\)
\(\displaystyle BC=4\sqrt{7}\small.\)
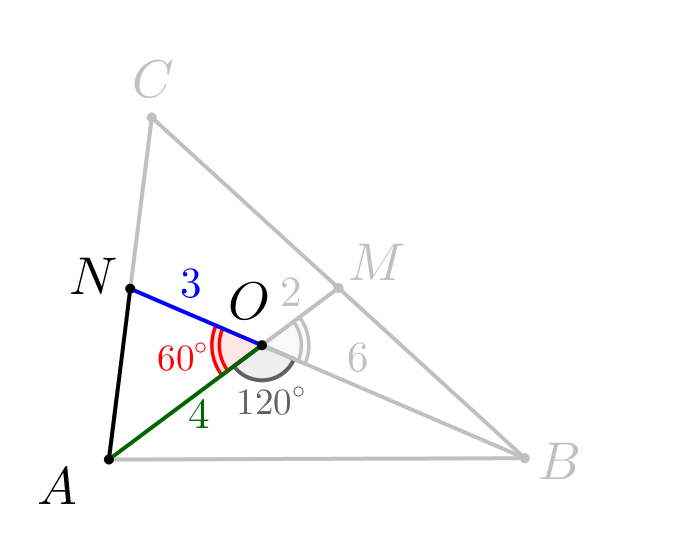
Рассмотрим треугольник \(\displaystyle BOM\small.\) Углы \(\displaystyle MOB\) и \(\displaystyle BOA\) вместе образуют развернутый угол. Тогда \(\displaystyle \angle MOB=180^{\circ}-\angle BOA=180^{\circ}-120^{\circ}=60^{\circ}\small.\)
\(\displaystyle BM^2=MO^2+BO^2-2\cdot MO\cdot BO\cdot\cos60^{\circ}\small.\) Подставим известные значения: \(\displaystyle BM^2=2^2+6^2-2\cdot2\cdot6\cdot\frac{1}{2}=28\small,\) \(\displaystyle BM=\sqrt{28}=2\sqrt{7}\small.\) | 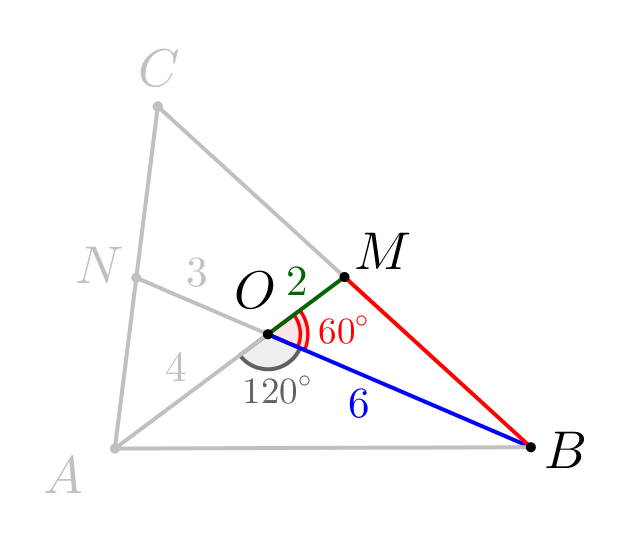 |
Точка \(\displaystyle M\) делит сторону \(\displaystyle BC\) пополам, значит,
\(\displaystyle BC=2BM=2\cdot2\sqrt{7}=4\sqrt{7}\small.\)
\(\displaystyle AC=2\sqrt{13}\small.\)