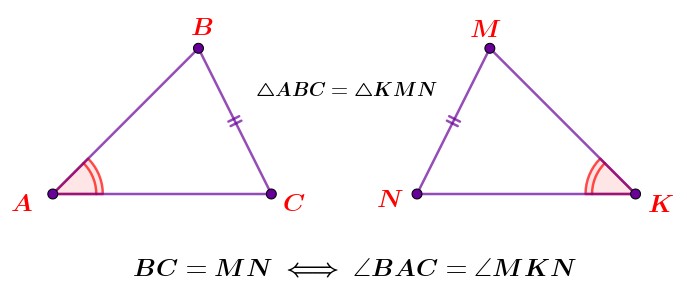
В двух треугольниках отметили равные элементы.
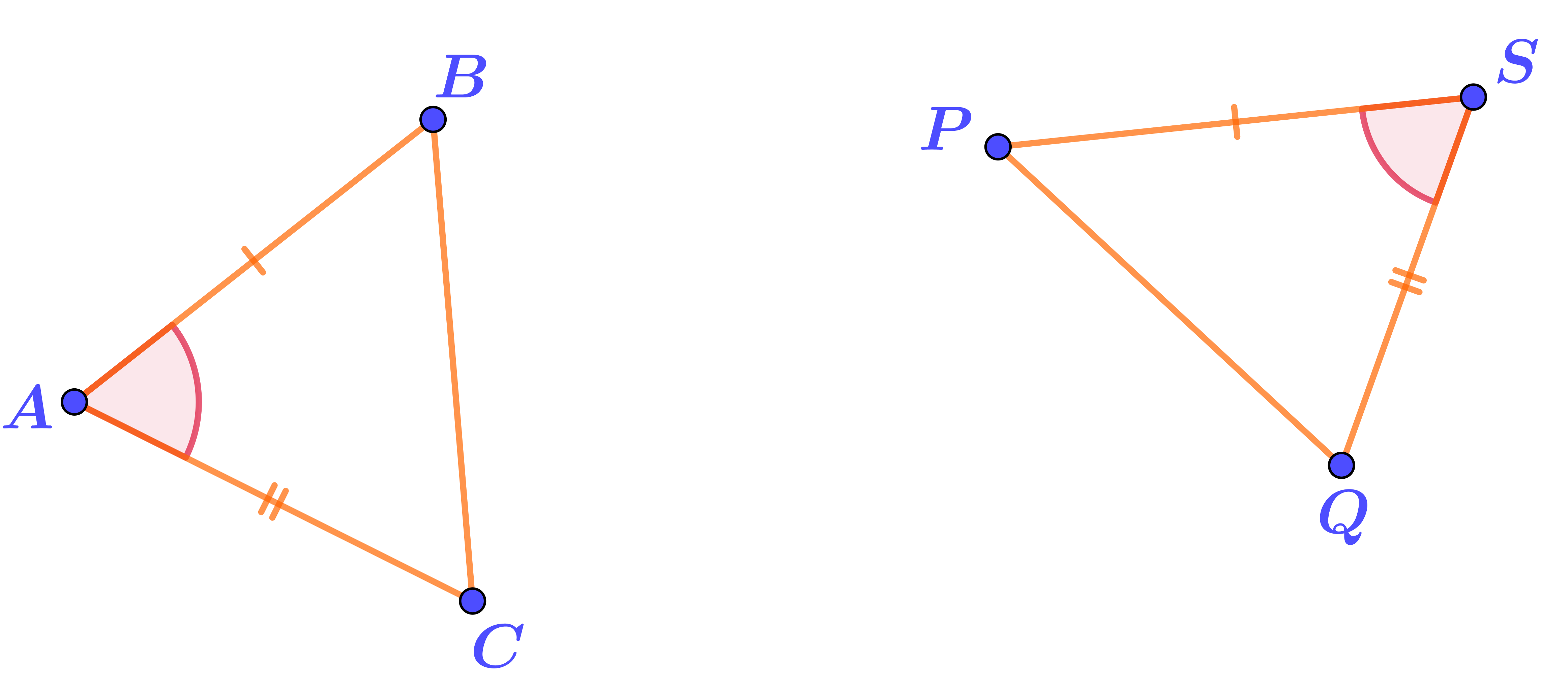
Сопоставьте трём элементам треугольника \(\displaystyle ABC\) равные им элементы треугольника \(\displaystyle PQS{\small .}\)
| \(\displaystyle BC\) | \(\displaystyle =\) | |
| \(\displaystyle {\bf\angle}ABC\) | \(\displaystyle =\) | |
| \(\displaystyle {\bf\angle}ACB\) | \(\displaystyle =\) |
1. Треугольники \(\displaystyle ABC\) и \(\displaystyle PQS\)равны по первому признаку:
\(\displaystyle \left\{\begin{array}{ll}AB=SP\\AC=SQ\\\angle BAC=\angle PSQ\end{array}{\LARGE\Rightarrow}\quad\begin{array}{c} \\{\bf\triangle}ABC={\bf\triangle}SPQ\\\text{ \footnotesize\it(по первому признаку)}\end{array}\right.\)
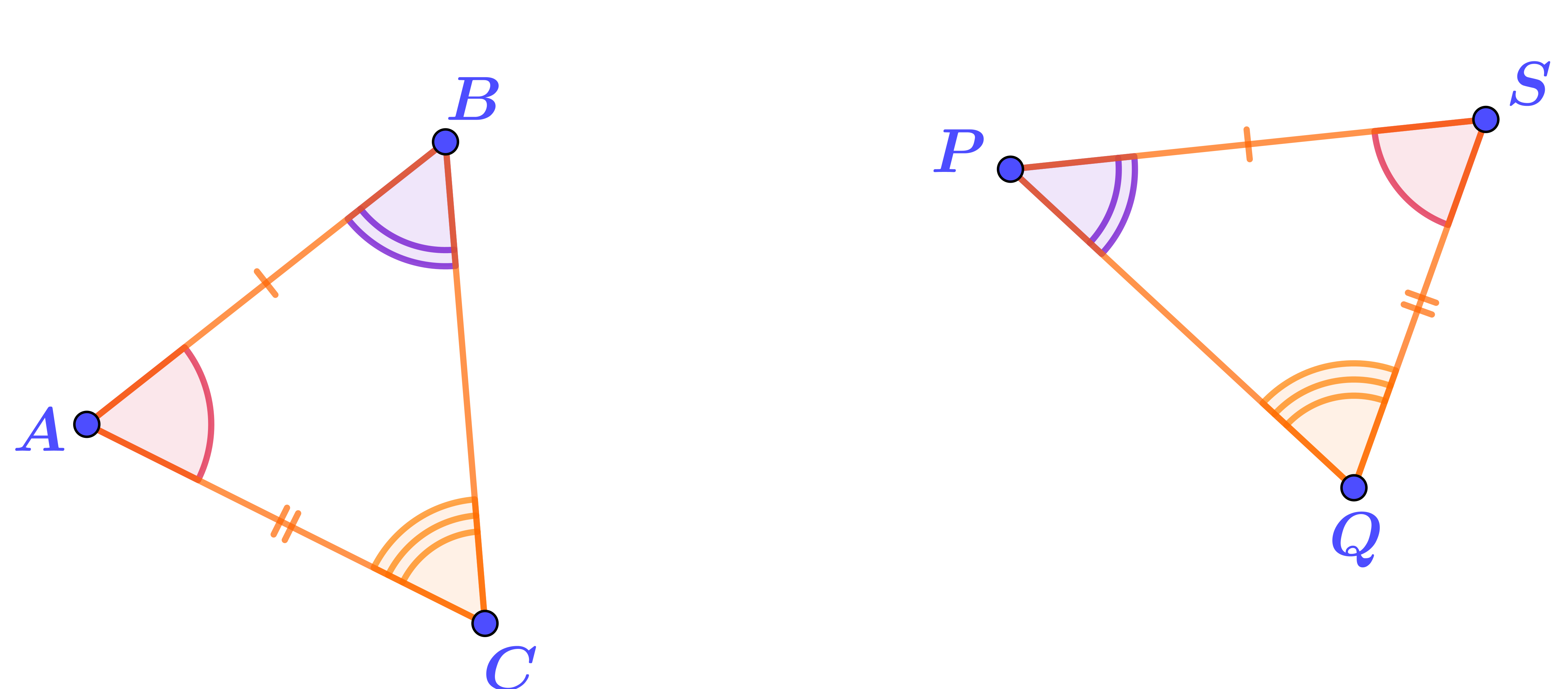
На полученном рисунке сопоставим элементам треугольника \(\displaystyle ABC\) равные им элементы треугольника \(\displaystyle PQS{\small .}\)
| \(\displaystyle BC\) | \(\displaystyle =\) | \(\displaystyle PQ\) |
| \(\displaystyle {\bf\angle}ABC\) | \(\displaystyle =\) | \(\displaystyle {\bf\angle}SPQ\) |
| \(\displaystyle {\bf\angle}ACB\) | \(\displaystyle =\) | \(\displaystyle {\bf\angle}PQS\) |
Ответ:\(\displaystyle BC=PQ{\small ,}\) \(\displaystyle {\bf\angle}ABC={\bf\angle}SPQ{\small ,}\)\(\displaystyle {\bf\angle}ACB={\bf\angle}PQS{\small .}\)