На общем основании построены треугольники \(\displaystyle ABC\) и \(\displaystyle ADC{\small .}\) Отрезки \(\displaystyle AD\) и \(\displaystyle BC\) пересекаются в точке \(\displaystyle O{\small .}\)
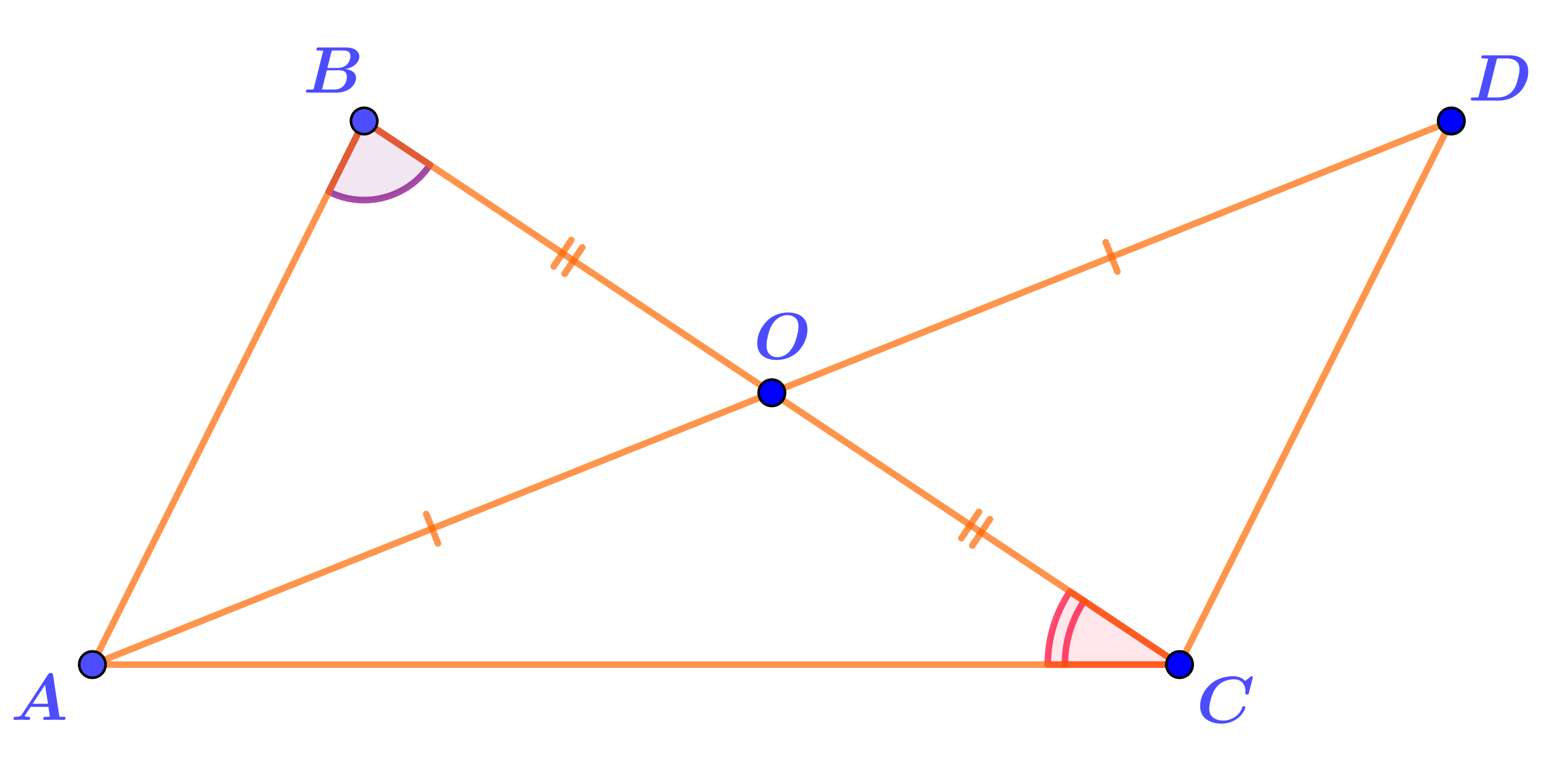
На рисунке отмечены равные отрезки.
Даны величины двух углов: \(\displaystyle \angle ABC=72\degree \) и \(\displaystyle \angle ACB=47\degree{\small .}\)
Найдите величину угла \(\displaystyle ACD {\small .}\)
\(\displaystyle \angle ACD=\) \(\displaystyle \degree \)
Величина угла \(\displaystyle ACD\) равна сумме величин его частей:
\(\displaystyle \angle ACD=\angle ACB+\angle BCD{\small .}\)
Величина угла \(\displaystyle \angle ACB\) известна по условию.
Неизвестна величина угла \(\displaystyle \angle BCD{\small .}\) Нужно найти угол известной меры, равный углу \(\displaystyle \angle BCD{\small .}\)
1. Докажем, что равны треугольники \(\displaystyle AOB\) и \(\displaystyle DOC{\small .}\)
В этих треугольниках даны две пары равных сторон.
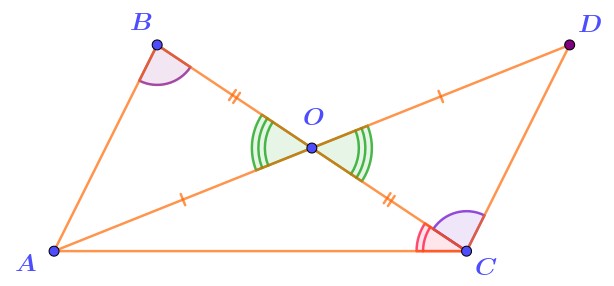
Запись доказательства равенства треугольников:
\(\displaystyle \left\{\begin{array}{ll}OB=OC\\OA=OC\\\angle AOB=\angle DOC\text{ \footnotesize\it(как вертикальные)}\end{array}{\LARGE\Rightarrow}\quad\begin{array}{c} \\{\bf\vartriangle}ACN={\bf\vartriangle}BCM\\\text{ \footnotesize\it(по первому признаку)}\end{array}\right.\)
2. Из равенства треугольников следует равенство углов, расположенных против равных сторон \(\displaystyle AO\) и \(\displaystyle DO{\small :}\)
\(\displaystyle \angle DCO=\angle ABO=72\degree{\small .}\)
3. Получим величину угла \(\displaystyle ACD{\small ,}\) как сумму величин его частей.
\(\displaystyle \angle ACD= \angle ACO+\angle OCD=47\degree +72\degree =\)\(\displaystyle \bf 119\degree{\small .} \)
Ответ: \(\displaystyle 119\degree{\small .}\)