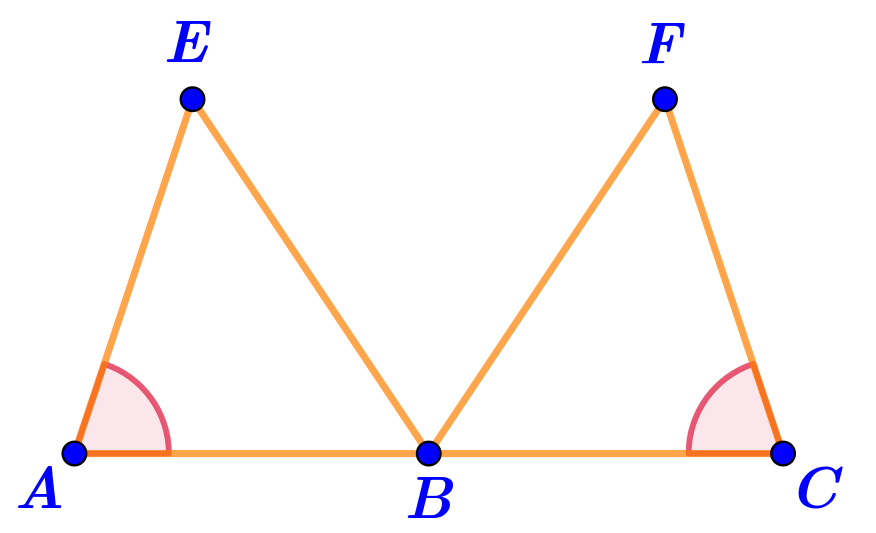
Точки \(\displaystyle E\) и \(\displaystyle F\) соединены с концами отрезка \(\displaystyle AC\) и с точкой \(\displaystyle B{\small ,}\) принадлежащей ему.
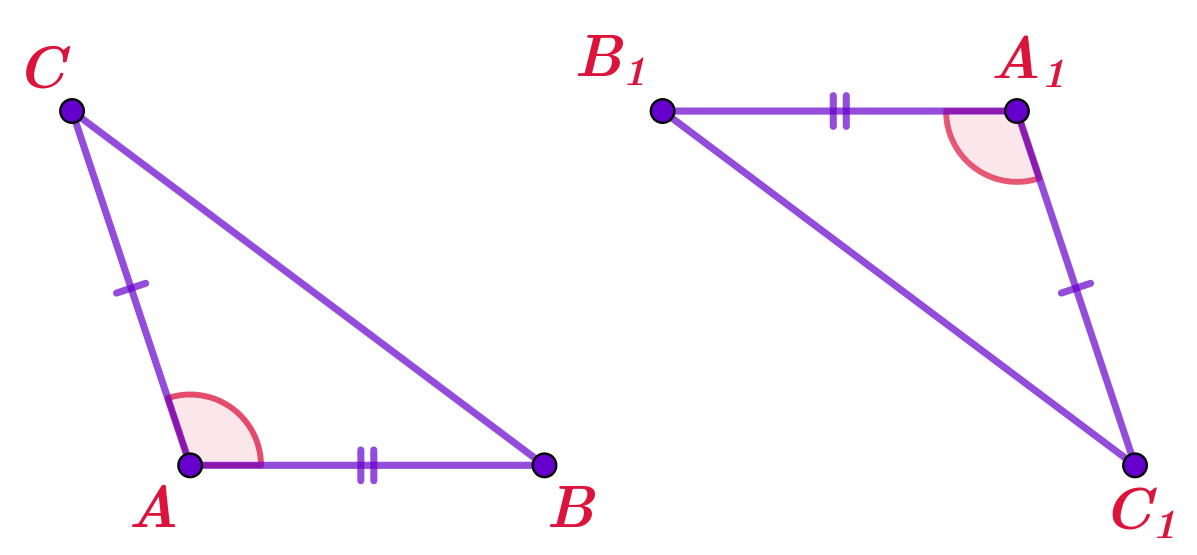
На рисунке отмечены равные углы.
Известны длины отрезков: \(\displaystyle AE=7{\small ,\;}AB=6{\small ,\;}AC=12{\small ,\;}CF=7{\small .}\)
Найти величину угла \(\displaystyle EBF{\small ,}\) если угол \(\displaystyle ABE\) составляет \(\displaystyle 52\degree {\small .}\)
\(\displaystyle \angle EBF=\)\(\displaystyle \degree\)
Нужно доказать, что треугольники \(\displaystyle EAB\) и \(\displaystyle FCB\) равны.
Тогда будет известна величина их равных углов при вершине \(\displaystyle B{\small .}\)
1. Отметим на рисунке отрезки равной длины:
- \(\displaystyle AE=CF=7\) по условию;
- \(\displaystyle BC=AC-AB=12-6=6\), значит \(\displaystyle AB=BC=6{\small .}\)

2. Рассмотрим треугольники \(\displaystyle EAB\) и \(\displaystyle FCB{\small .}\)
Доказательство равенства можно записать так:
\(\displaystyle \left\{\begin{array}{ll}AE=CF\\AB=CB\\\angle EAB=\angle FCB\end{array}{\LARGE\Rightarrow}\quad\begin{array}{c} \\{\bf\triangle}EAB={\bf\triangle}FCB\\\text{ \footnotesize\it(по первому признаку)}\end{array}\right.\)
3. В равных треугольниках равны углы, расположенные против равных сторон. Значит:
\(\displaystyle \angle CBF=\angle ABE=52\degree{\small .}\)
4. Развёрнутый угол \(\displaystyle ABC\) состоит из углов \(\displaystyle ABE{\small ,\;}EBF\) и \(\displaystyle CBF{\small .}\)
Его величина равна сумме величин его равных частей:
\(\displaystyle \angle ABE+\angle EBF+\angle CBF=180\degree {\small .}\)
Подставим в это равенство все известные величины:
\(\displaystyle 52\degree+\angle EBF+52\degree=180\degree {\small .}\)
Откуда
\(\displaystyle \angle EBF=180\degree -104\degree=76\degree {\small .}\)
Ответ: \(\displaystyle \angle EBF=76\degree {\small .}\)