В выпуклом четырёхугольнике \(\displaystyle ABCD{\small:}\)
\(\displaystyle \angle BAC=44^{\circ}{\small,}\) \(\displaystyle \angle BCA=38^{\circ}{\small,}\) \(\displaystyle \angle DAC=44^{\circ}{\small,}\) \(\displaystyle \angle DCA=38^{\circ}{\small.}\)
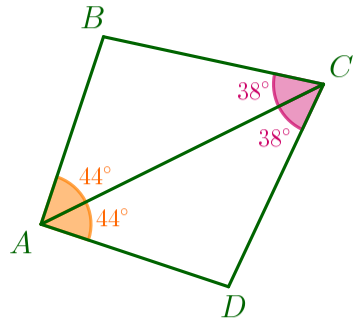
Является ли данный четырёхугольник параллелограммом?
| Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны. |  |
Проверим, параллельны ли противоположные стороны данного четырёхугольника \(\displaystyle ABCD{\small.}\)
Рассмотрим прямые \(\displaystyle AD\) и \(\displaystyle BC{\small.}\)
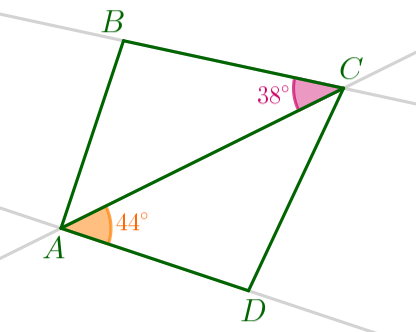 |
|
| Если две прямые пересечены секущей и накрест лежащие углы равны, то эти прямые параллельны. | 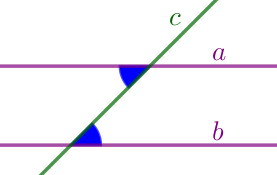 |
По условию, \(\displaystyle \angle BCA=38^{\circ}{\small,}\) \(\displaystyle \angle DAC=44^{\circ}{\small.}\) То есть накрест лежащие углы не равны:
\(\displaystyle \angle BCA\, \, \cancel=\, \, \angle DAC{\small.}\)
Значит, прямые \(\displaystyle AD\) и \(\displaystyle BC\) не параллельны.
Следовательно, четырёхугольник \(\displaystyle ABCD\) не является параллелограммом.
Ответ: Нет.