На рисунке три параллельные прямые \(\displaystyle a{\small,}\) \(\displaystyle b\) и \(\displaystyle c\) пересечены тремя параллельными прямыми \(\displaystyle m{\small,}\) \(\displaystyle n\) и \(\displaystyle l{\small.}\) Точки пересечения обозначены буквами.

Сколько всего параллелограммов с вершиной в точке \(\displaystyle A\) изображено на рисунке?
| Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны. |  |
Если два отрезка лежат на параллельных прямых или на одной прямой, то эти отрезки параллельны.
Найдём на рисунке все параллелограммы и посчитаем их количество:
| рисунок | параллелограмм | количество |
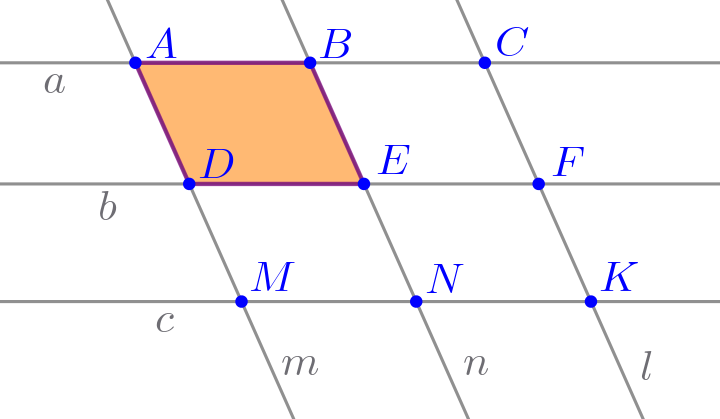 | \(\displaystyle \color{blue}{ABED}\)
| \(\displaystyle \color{red}{1}\) |
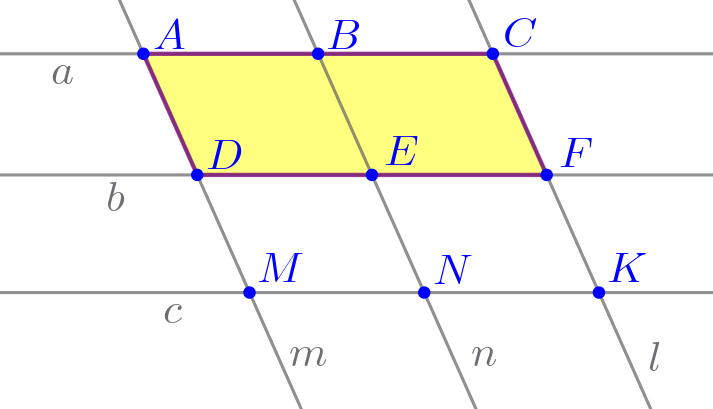 | \(\displaystyle \color{blue}{ACFD}\)
| \(\displaystyle \color{red}{1}\) |
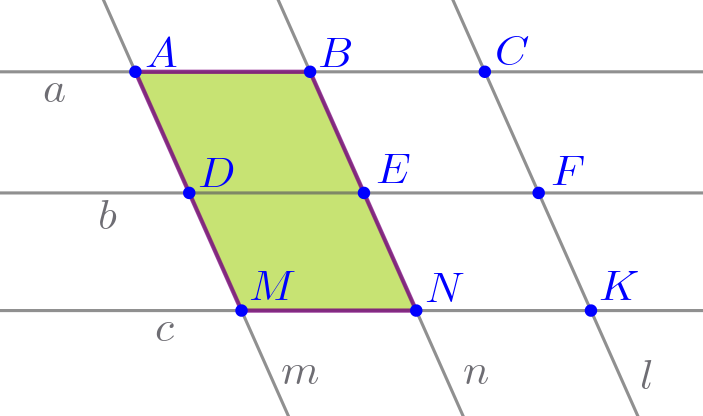 | \(\displaystyle \color{blue}{ABNM}\)
| \(\displaystyle \color{red}{1}\) |
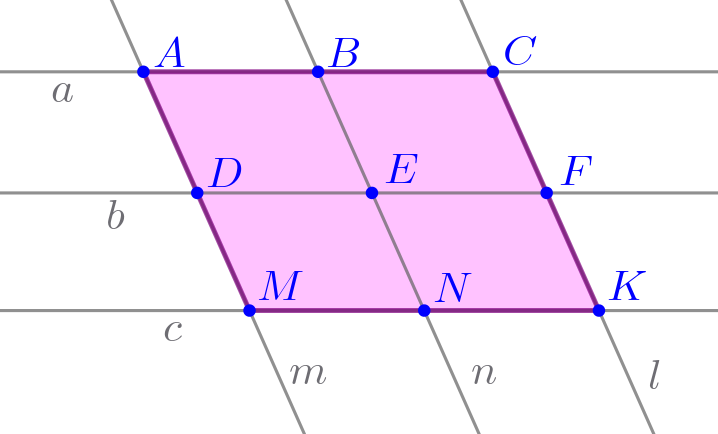 | \(\displaystyle \color{blue}{ACKM}\)
| \(\displaystyle \color{red}{1}\) |
Получаем:
\(\displaystyle 1+1+1+1=4{\small.} \)
На данном рисунке изображено \(\displaystyle 4\) параллелограмма с вершиной в точке \(\displaystyle A\).
Ответ: \(\displaystyle 4{\small.}\)