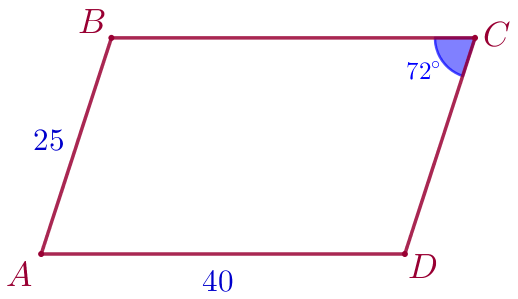
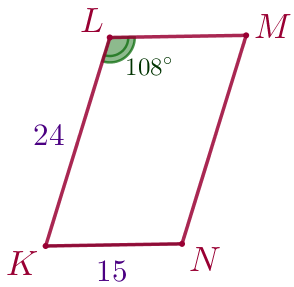
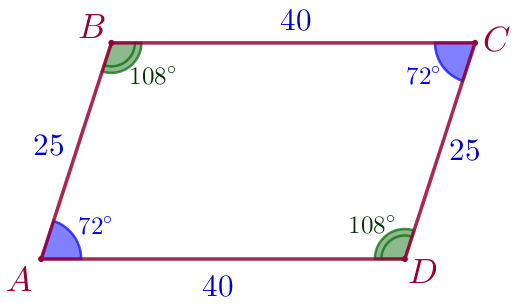
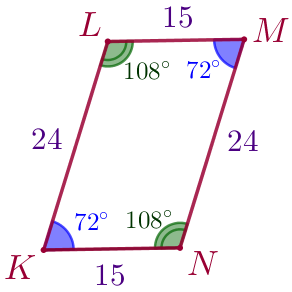
В параллелограмме \(\displaystyle ABCD\) угол \(\displaystyle C\) равен \(\displaystyle 72^{\circ}{\small,}\) а стороны \(\displaystyle AB\) и \(\displaystyle AD\) равны \(\displaystyle 25\) и \(\displaystyle 40\) соответственно. В параллелограмме \(\displaystyle KLMN\) угол \(\displaystyle L\) равен \(\displaystyle 108^{\circ}{\small,}\) а стороны \(\displaystyle KL\) и \(\displaystyle KN\) равны \(\displaystyle 24\) и \(\displaystyle 15\) соответственно.
Верно ли, что эти параллелограммы подобны?
Выполним построение по условию задачи и рассмотрим параллелограммы \(\displaystyle ABCD\) и \(\displaystyle KLMN{\small.}\)
В параллелограмме \(\displaystyle ABCD{\small:}\)
|
В параллелограмме \(\displaystyle KLMN{\small:}\)
|
- сначала определить, какие углы являются соответственными – они должны быть равны;
- затем по сторонам соответственных и равных углов определить, какие стороны соответственны – они должны быть пропорциональны.
По свойствам в параллелограмме противоположные стороны попарно равны и противоположные углы попарно равны. Обозначим равные измерения на рисунке.
В параллелограмме \(\displaystyle ABCD{\small:}\)
|
В параллелограмме \(\displaystyle KLMN{\small:}\)
|
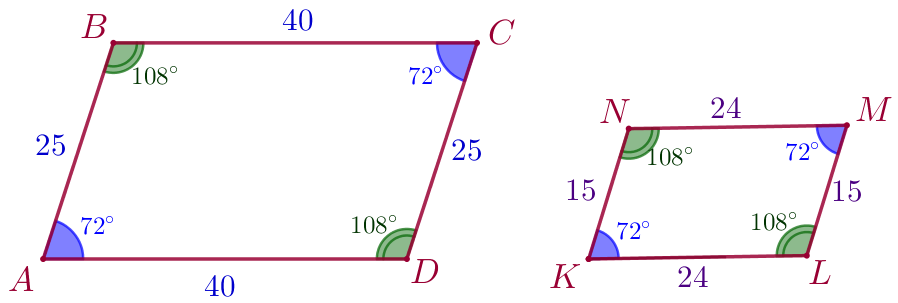
Заметим, что:
\(\displaystyle 1)\) острые углы данных параллелограммов соответственно равны и тупые углы соответственно равны;
\(\displaystyle 2)\) отношение больших сторон параллелограммов \(\displaystyle ABCD\) и \(\displaystyle KLMN\) равно отношению меньших сторон этих параллелограммов.
Получили:
- большие и меньшие углы данных параллелограммов являются соответственными и они равны;
- большие и меньшие стороны при этих углах являются соответственными и они пропорциональны.
Значит, параллелограммы \(\displaystyle ABCD\) и \(\displaystyle KLMN\) подобны.
Ответ: Да.