Найдите площадь прямоугольника, если его периметр равен \(\displaystyle 18\) и одна сторона на \(\displaystyle 3\) больше другой.
Сначала найдем стороны прямоугольника.
Пусть \(\displaystyle AB=x\) – меньшая сторона прямоугольника, тогда \(\displaystyle AD=x+3\) – большая сторона прямоугольника.
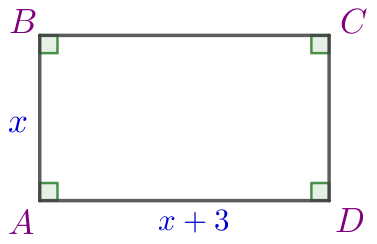
Периметр прямоугольника равен \(\displaystyle P=2(AB+AD).\) Известно, что \(\displaystyle P=18.\)
Значит,
\(\displaystyle 2(x+x+3)=18,\)
\(\displaystyle 2(2x+3)=18 \, | :\color{red}{2},\)
\(\displaystyle 2x+3=9,\)
\(\displaystyle 2x=6 \, | :\color{red}{2},\)
\(\displaystyle x=3.\)
Таким образом, стороны прямоугольника равны \(\displaystyle 3\) и \(\displaystyle 6.\) Тогда площадь прямоугольника равна
\(\displaystyle S=AB\cdot AD=3\cdot 6 =18\).
Ответ: \(\displaystyle 18{\small .}\)