Найдите сторону квадрата, площадь которого равна площади прямоугольника со смежными сторонами \(\displaystyle 12\, {\footnotesize см}\) и \(\displaystyle 27\, {\footnotesize см}{\small.}\)
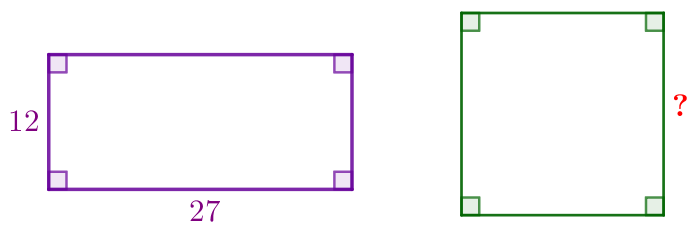
\(\displaystyle {\footnotesize см}{\small.}\)
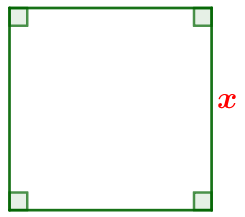 | Пусть \(\displaystyle \color{red}{x}\) – сторона квадрата. Площадь квадрата равна квадрату его стороны, то есть \(\displaystyle S_{кв}=\color{red}{x}^2 {\small.}\) |
 | Площадь прямоугольника равна произведению его смежных сторон, то есть \(\displaystyle S_{пр}=12 \cdot 27=324{\small.}\) |
По условию площадь квадрата равна площади данного прямоугольника, то есть
\(\displaystyle \color{red}{x}^2=324{\small.}\)
Так как длина стороны квадрата положительна, то
\(\displaystyle \color{red}{x}=18{\small.}\)
Ответ: \(\displaystyle 18\, {\footnotesize см}{\small.}\)