Skip to main content

Теория: 08 Отношение площадей подобных треугольников

Задание

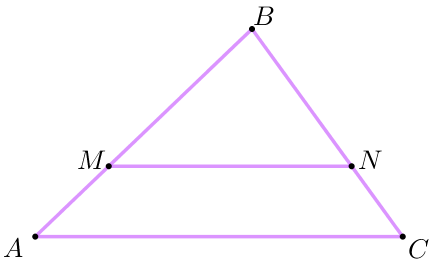
Прямая, параллельная стороне \(\displaystyle AC\) треугольника \(\displaystyle ABC {\small,}\) пересекает стороны \(\displaystyle AB\) и \(\displaystyle BC\) в точках \(\displaystyle M\) и \(\displaystyle N\) соответственно, \(\displaystyle AC=36 {\small,}\) \(\displaystyle MN=27 {\small.}\) Площадь треугольника \(\displaystyle ABC\) равна \(\displaystyle 96 {\small.}\)Найдите площадь треугольника \(\displaystyle MBN{\small.}\)

Решение

Так как \(\displaystyle MN \parallel AC {\small,} \) \(\displaystyle AB\) – секущая, то \(\displaystyle \angle BMN= \angle BAC\) \(\displaystyle (\)как соответственные\(\displaystyle ){\small.}\)

 

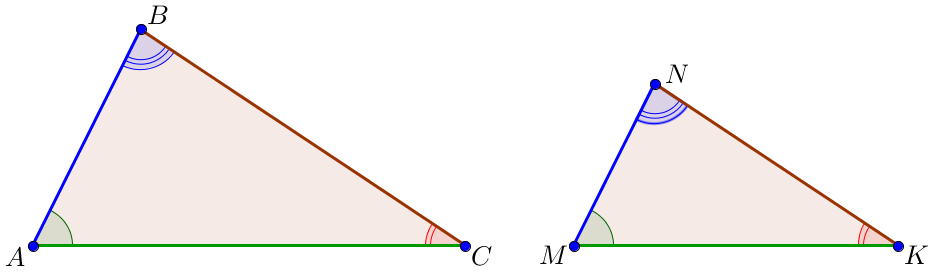
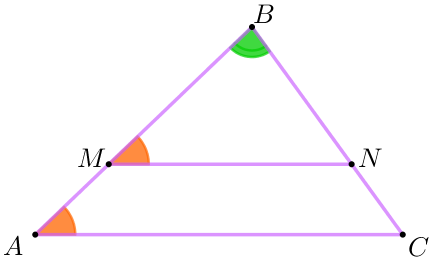Рассмотрим треугольники \(\displaystyle MBN\) и \(\displaystyle ABC {\small:} \\ \)

  •  \(\displaystyle \angle MBN= \angle ABC {\small,} \\ \)
  •  \(\displaystyle \angle BMN= \angle BAC {\small.}\)

Треугольники \(\displaystyle MBN\) и \(\displaystyle ABC \) подобны по двум углам.

В подобных треугольниках коэффициент подобия \(\displaystyle k\) равен отношению сходственных сторон:

\(\displaystyle k=\frac{MN}{AC}=\frac{27}{36} =\frac{3}{4}{\small.} \)

 

 

По теореме об отношении площадей подобных треугольников:

\(\displaystyle \frac{S_{\triangle MBN}}{S_{\triangle ABC}}=k^2 {\small,} \\ \)

\(\displaystyle S_{\triangle MBN}=k^2 \cdot {S_{\triangle ABC}}{\small,} \\ \)

\(\displaystyle S_{\triangle MBN}={\bigg( \frac{3}{4} \bigg)}^2 \cdot 96=\frac{9}{16}\cdot 96=54{\small.} \\ \)

Ответ: \(\displaystyle 54{\small.}\)