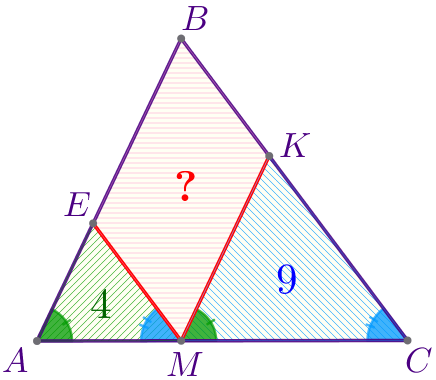
Треугольник разрезали на параллелограмм и два треугольника, площади которых равны \(\displaystyle 4\) и \(\displaystyle 9{\small.}\) Найдите площадь параллелограмма.
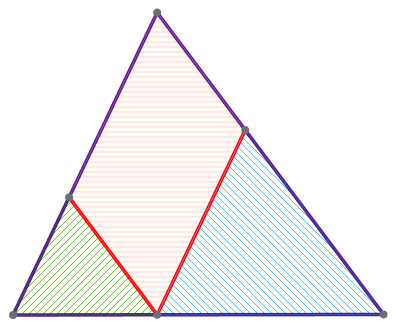
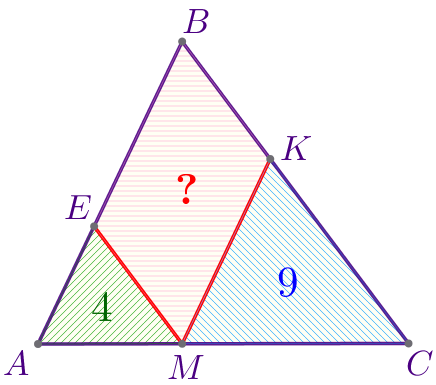 | \(\displaystyle ABC\) – треугольник:
|
Требуется найти площадь параллелограмма \(\displaystyle MEBK{\small.}\)
\(\displaystyle S_{\triangle ABC}=S_{MEBK}+S_{\triangle AEM}+S_{\triangle MKC}{\small.}\)
Тогда
\(\displaystyle S_{MEBK}=S_{\triangle ABC}-S_{\triangle AEM}-S_{\triangle MKC}{\small.}\)
Так как противоположные стороны параллелограмма параллельны, то
|
|
Следовательно, треугольники \(\displaystyle AEM{\small,}\) \(\displaystyle MKC\) и \(\displaystyle ABC\) подобны по двум углам.
Пусть \(\displaystyle \triangle AEM\) подобен \(\displaystyle \triangle MKC\) с коэффициентом \(\displaystyle k{\small.}\)
По теореме об отношении площадей подобных треугольников
\(\displaystyle \frac{S_{\triangle AEM}}{S_{\triangle MKC}}=\frac{4}{9}=k^2{\small.}\)
Значит,
\(\displaystyle k=\frac{2}{3}{\small.}\)
Стороны \(\displaystyle AM\) и \(\displaystyle MC\) этих треугольников являются сходственными.
Так как отношение сходственных сторон подобных треугольников равно коэффициенту подобия, то
\(\displaystyle \frac{AM}{MC}=\frac{2}{3}{\small.}\)
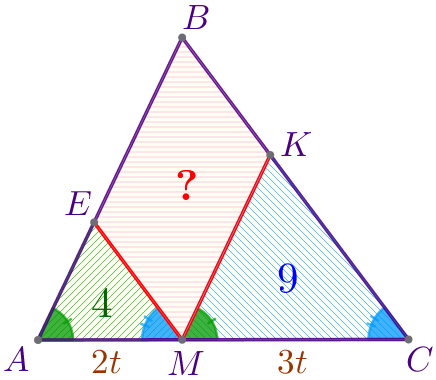 | Обозначим \(\displaystyle AM=2t{\small,}\) \(\displaystyle MC=3t{\small,}\) тогда \(\displaystyle AC=AM+MC=2t+3t=5t{\small.}\) |
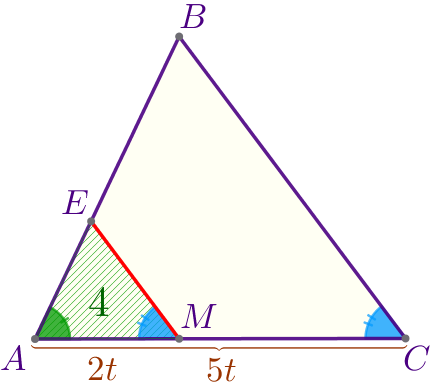 |
Найдём коэффициент подобия \(\displaystyle p\) треугольников \(\displaystyle AEM\) и \(\displaystyle ABC{\small:}\) \(\displaystyle p=\frac{AM}{AC}=\frac{2t}{5t}=\frac{2}{5}{\small.}\) |
По теореме об отношении площадей подобных треугольников
\(\displaystyle \frac{S_{\triangle AEM}}{S_{\triangle ABC}}=p^2=\left(\frac{2}{5}\right)^2=\frac{4}{25}{\small.}\)
Подставим \(\displaystyle S_{\triangle AEM}=4{\small:}\)
\(\displaystyle \frac{4}{S_{\triangle ABC}}=\frac{4}{25}{\small.}\)
По свойству пропорции
\(\displaystyle S_{\triangle ABC}=\frac{4 \cdot 25}{4}=25{\small.}\)
В результате получаем
\(\displaystyle S_{MEBK}=S_{\triangle ABC}-S_{\triangle AEM}-S_{\triangle MKC}=25-4-9=12{\small.}\)
Ответ: \(\displaystyle 12{\small.}\)